| Algorithm | Average | Worst Case |
| Space | O(n) | O(n) |
| Search | O(n) | O(n) |
| Insert | O(1) | O(log n) |
| Delete | O(1) | O(1) |
A simple tree data structure that typically uses an array to store values, rather than linked nodes. There are regularly two strategies with heaps, either they are a max or a min heap, where the root value is the maximum or the minimum, respectively.
Also referred to as priority queues – as they prioritize removing the maximum and inserting.
The height of a complete binary tree of size N is floor(lg N)
Given a well formed binary heap, the following locations relative to node k can be calculated easily:
- parent of k: [k/2]
- child 1 of k: [2k]
- child 2 of k: [2k+1]
Although the underlying structure of binary heap is typically an array, it can be helpful to think of it as a tree, where each node has two children. The invariant in this case is that the parent node is always larger than the two children nodes. To preserve this, whenever a new node is added, one of two processes occur to restore the heap order, both known as reheapifying.
Bottom-up reheapify (swim) occurs when a node’s value is increased to be larger than its parent or a new node is added at the bottom. Recursively replace the node with its parent until you hit a parent that is larger (or the root of the tree).
Top-down reheapify (sink) occurs when a node’s value is decreased or we replace the root node with something smaller. Recursively replace the larger of the two children with the parent until both children are smaller.
Custom Implementation
There are some interesting implementation details to pay attention to in order to get this right.
- Insert the first element at index 1 in the array not index 0. This helps simplify the calculation of parent / children location. For example, if we started with 0, to calculate the first child of the max element would be 2 * 0 = 0, which is incorrect. When starting at index 1, 2 * 1 = 2, bingo!
- Make sure when sinking, you compare parents to both their children to decide what to swap and choose the largest child.
#include <memory>
#include <iostream>
#include <optional>
#include <utility>
#include <cstring>
template<typename T>
class BinaryHeap {
public:
BinaryHeap(int capacity = 10) :
m_capacity(capacity) {
m_buffer = std::make_unique<T[]>(m_capacity);
}
void insert(T key) {
int idx = m_tail++;
resizeBuffer();
m_buffer[idx] = key;
swim(idx); // bottom-up reheapify
}
std::optional<T> delMax() {
if(!size())
return std::nullopt; // or {}, which will initialise std::optional with no arguments
T max = m_buffer[1];
m_tail--;
if(size() > 0) {
m_buffer[1] = m_buffer[m_tail];
sink(1);
}
return max;
}
int size() { return m_tail - 1; }
void printBuffer() {
for(int i = 1; i<m_tail; i++) {
std::cout << m_buffer[i] << ' ';
}
std::cout << std::endl;
}
private:
void swim(int lowIdx) {
int highIdx = lowIdx / 2;
while(highIdx > 0) { // this is why we start with m_tail = 1 :)
if(m_buffer[highIdx] < m_buffer[lowIdx])
std::swap(m_buffer[highIdx], m_buffer[lowIdx]);
lowIdx = highIdx;
highIdx /= 2;
}
}
void sink(int parentIdx) {
int childBaseIdx = parentIdx * 2;
while(childBaseIdx < m_tail - 1) {
int swapIdx = parentIdx;
if(m_buffer[childBaseIdx] > m_buffer[parentIdx])
swapIdx = childBaseIdx;
childBaseIdx++;
if(childBaseIdx < m_tail &&
m_buffer[childBaseIdx] > m_buffer[parentIdx] &&
m_buffer[childBaseIdx] > m_buffer[swapIdx])
swapIdx = childBaseIdx;
if(swapIdx != parentIdx)
std::swap(m_buffer[parentIdx], m_buffer[swapIdx]);
parentIdx = swapIdx;
childBaseIdx = parentIdx * 2;
}
}
void resizeBuffer() {
float occupancy = static_cast<float>(size()) / m_capacity;
if(occupancy > 0.75) {
std::cout << "resizing" << std::endl;
m_capacity *= 2;
std::unique_ptr<T[]> resized = std::make_unique<T[]>(m_capacity);
memcpy(resized.get(), m_buffer.get(), size() * sizeof(T));
m_buffer = std::move(resized);
}
}
int m_capacity;
int m_tail = 1;
std::unique_ptr<T[]> m_buffer;
};STL Implementation
The STL has the make_heap(), pop_heap(), and push_heap() to work with heaps, as described here. You can use it with a vector. make_heap() will reorganise the elements into a heap structure. If you want to add an element, add it to the end of the vector and use push_heap() to perform bottom-up reheapifying. If you want to remove the max element, first call pop_heap(). This will reduce the size of the vector considered to be a heap by one, and place the previous maximum element at the end of the vector.
#include <iostream>
#include <algorithm>
#include <vector>
using namespace std;
int main(int argc, char* argv[]) {
vector<int> data = {100, 33, 70, 8, 1, 6};
// data is now structured as a heap
make_heap(data.begin(), data.end());
cout << "Max element is: " << data.front() << endl;
/*
* Removing the max element:
* We call pop_heap() first. This removes the max element
* by putting it into last-1 position of the vector then reducing
* the part of the vector considered to be a heap by one. The new par
* considered to be a heap will be [0:-2].
*/
pop_heap(data.begin(), data.end());
data.pop_back();
cout << "New max element is: " << data.front() << endl;
/*
* Inserting an element:
* We push the desired element onto the end of the vector, then
* call push_heap() to perform the bottom up reheapifying.
*/
data.push_back(101);
push_heap(data.begin(), data.end());
cout << "New max element is: " << data.front() << endl;
return 0;
}The STL also has priority_queue. This simplifies a priority queue or binary heap by providing push() (which effectively calls vec.push_back(value); push_heap(vec.begin(), vec.end());) and pop() (which effectively calls pop_heap(c.begin(), c.end()); c.pop_back();). For example:
#include <iostream>
#include <queue>
#include <vector>
using namespace std;
int main(int argc, char* argv[]) {
vector<int> testData = {33, 100, 300, 30, 20, 7, 8};
// max heap - default instantiation
priority_queue<int, vector<int>, less<int>> max_pq;
for(auto td : testData)
max_pq.push(td);
cout << "Max heap:" << endl;
while(max_pq.size()) {
cout << max_pq.top() << endl;
max_pq.pop();
}
// min heap
priority_queue<int, vector<int>, greater<int>> min_pq;
for(auto td : testData)
min_pq.push(td);
cout << "Min heap:" << endl;
while(min_pq.size()) {
cout << min_pq.top() << endl;
min_pq.pop();
}
// Custom data type with lambda function, just for fun
struct CustomType {
int data = 0;
};
vector<CustomType> custom_testData = {{33}, {100}, {300}, {20}};
// obviously, it would be better to override operator< for CustomeType
auto CustomTypeComparator = [](CustomType& L, CustomType& R) { return L.data < R.data; };
priority_queue<CustomType, vector<CustomType>, decltype(CustomTypeComparator)> custom_pq(CustomTypeComparator);
for(auto ctd : custom_testData)
custom_pq.push(ctd);
cout << "Custom comparator heap" << endl;
while(custom_pq.size()) {
cout << custom_pq.top().data << endl;
custom_pq.pop();
}
return 0;
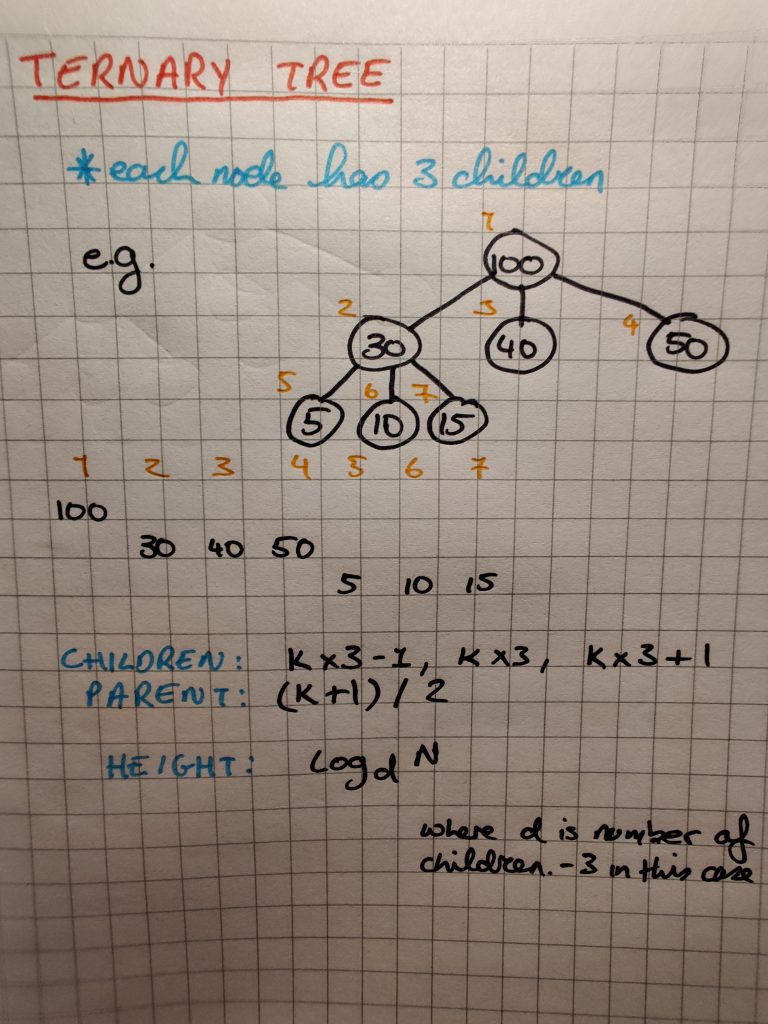
}Ternary Tree
Depending on the underlying data, it might make sense to increase the number of children per node in the “tree”. This will have the effect of reducing the height of the tree, which will logd N, where d is the number of children. The structure is very similar, but the arithmetic is slightly different (please forgive my terrible drawing):