Two Pointers
Prompt:
You are given an integer array
numsand an integerk.In one operation, you can pick two numbers from the array whose sum equals
kand remove them from the array.Return the maximum number of operations you can perform on the array.
Example 1:
Input: nums = [1,2,3,4], k = 5 Output: 2 Explanation: Starting with nums = [1,2,3,4]: - Remove numbers 1 and 4, then nums = [2,3] - Remove numbers 2 and 3, then nums = [] There are no more pairs that sum up to 5, hence a total of 2 operations.
Notes:
- Sort array
- 2 pointers, starting beginning and end
- Then we know if current sum > k, need a small number, can decrement right pointer (and vice versa)
Given two strings
sandt, returntrueifsis a subsequence oft, orfalseotherwise.A subsequence of a string is a new string that is formed from the original string by deleting some (can be none) of the characters without disturbing the relative positions of the remaining characters. (i.e.,
"ace"is a subsequence of"abcde"while"aec"is not).
class Solution {
public boolean isSubsequence(String s, String t) {
int sIdx = 0;
for (int tIdx = 0; tIdx < t.length() && sIdx < s.length(); tIdx++) {
if (t.charAt(tIdx) == s.charAt(sIdx)) {
sIdx++;
}
}
return sIdx == s.length();
}
}
Two Sum II – Input Array Is Sorted
- 2 pointers, start and end
- if sum > target, decrease end, otherwise increase left
- problem also stated array is 1-indexed
- Complexity O(n)
class Solution {
public int[] twoSum(int[] numbers, int target) {
int leftIdx = 0, rightIdx = numbers.length - 1;
while(leftIdx < rightIdx) {
int sum = numbers[leftIdx] + numbers[rightIdx];
if (sum == target) break;
else if (sum > target) rightIdx--;
else leftIdx++;
}
return new int[] {leftIdx+1, rightIdx+1};
}
}
Container With Most Water
You are given an integer array
heightof lengthn. There arenvertical lines drawn such that the two endpoints of theithline are(i, 0)and(i, height[i]).Find two lines that together with the x-axis form a container, such that the container contains the most water.
Return the maximum amount of water a container can store.
Notice that you may not slant the container.
- Complexity O(n)
class Solution {
public int maxArea(int[] height) {
int left = 0, right = height.length - 1;
int maxArea = 0;
while(left < right && left < height.length && right > 0) {
maxArea = Math.max(maxArea, calcArea(height, left, right));
if (height[left] > height[right]) right--;
else left++;
}
return maxArea;
}
private int calcArea(int[] heights, int left, int right) {
int minHeight = Math.min(heights[left], heights[right]);
return minHeight * (right - left);
}
}
3Sum
Given an integer array nums, return all the triplets
[nums[i], nums[j], nums[k]]such thati != j,i != k, andj != k, andnums[i] + nums[j] + nums[k] == 0.Notice that the solution set must not contain duplicate triplets.
- Approach:
- sort array
- then iterate array using
i(skipping duplicates) - for each element create 2 pointers,
i + 1(left) andnums.length - 1(right) - apply 2 pointer sum approach to find elements that sum (left + right + 1) == 0
- note
- skip duplicates when moving pointers
- return empty if length < 3
- stop iterating main loop at
i < num.length - 2(for the 2 pointers to the right) - make sure to exit early when
nums[i] > 0
complexity:
- Sorting: O(n log n)
- Loops:
- outer loop, most 0(n) times
- inner loop, most O(n) times
- result -> O(n log n) + O(n*n) => O(n^2)
/**
Approach
- sort array
- then iterate array using i (skipping duplicates)
- for each element create 2 pointers, i + 1 (left) and nums.length - 1 (right)
- apply 2 pointer sum approach to find elements that sum (left + right + 1) == 0
- note skip duplicates when moving pointers
*/
class Solution {
public List<List<Integer>> threeSum(int[] nums) {
List<List<Integer>> ans = new ArrayList<List<Integer>>();
if (nums == null || nums.length < 3) return ans;
// sort to allow 2 pointer approach
Arrays.sort(nums);
// 0 .. nums.length - 2 because using 2 pointers to right of i
for (int i = 0; i < nums.length - 2; i++) {
// skip duplicates
if (i > 0 && nums[i] == nums[i-1]) continue;
// optimisation, as it's sorted, if nums[i] > 0, nums[i] plus anything on right will be greater than 0;
if (nums[i] > 0) break;
int left = i+1, right = nums.length - 1;
while (left < right) {
int sum = nums[i] + nums[left] + nums[right];
if (sum == 0) {
ans.add(new ArrayList<Integer>(List.of(nums[i], nums[left], nums[right])));
//advance
left++;
right--;
//skip dups
while(left < right && nums[left] == nums[left - 1]) left++;
while(left < right && nums[right] == nums[right + 1]) right--;
} else if (sum < 0) {
left++;
} else {
right--;
}
}
}
return ans;
}
}
Sliding Window
Summary
- Sliding window concept: Maintain a subarray (“window”) using two pointers,
leftandright; expand the window by movingright, and shrink it by movingleftwhen the window becomes invalid. - Window behavior: The window grows until it violates a constraint, then shrinks until it becomes valid again, continuously sliding to the right across the array.
- Example: For
nums = [3, 2, 1, 3, 1, 1]andk = 5, expanding the window gives[3, 2, 1]with sum6(invalid). Shrinking from the left removes3, resulting in[2, 1], which is valid again. - Why it works (positive numbers): With only positive integers, adding elements always increases the sum, so once a window is invalid, removing elements from the left is the only way to restore validity.
- Key insight: Once an element is removed from the left, it never needs to be reconsidered, since keeping it would only make future subarrays larger and invalid.
Lessons Learned
- Immediately after incrementing right, must correct the window to ensure window is still valid. In practice, this means the “shrinking” while loop is likely first statement within the “growing” for loop
Given an array of positive integers
numsand a positive integertarget, return the minimal length of a subarray whose sum is greater than or equal totarget. If there is no such subarray, return0instead.
class Solution {
private static final int INVALID_RESPONSE = 0;
public int minSubArrayLen(int target, int[] nums) {
if (target <= 0 || nums.length == 0) return INVALID_RESPONSE;
int minWindowSize = Integer.MAX_VALUE;
int left = 0, right = 0;
int windowSum = 0;
// grow window on the right
for (; right < nums.length; right++) {
windowSum += nums[right];
// shrink window on the left when violates target constraint
while (left <= right && windowSum >= target) {
minWindowSize = Math.min(minWindowSize, right - left + 1);
windowSum -= nums[left];
left++;
}
}
return minWindowSize == Integer.MAX_VALUE ? INVALID_RESPONSE : minWindowSize;
}
}
if we wanted to match target, use the following (note the different comparison ops)
class Solution {
private static final int INVALID_RESPONSE = 0;
public int minSubArrayLen(int target, int[] nums) {
if (target <= 0 || nums.length == 0) return INVALID_RESPONSE;
int minWindowSize = Integer.MAX_VALUE;
int left = 0, right = 0;
int windowSum = 0;
// grow window on the right
for (; right < nums.length; right++) {
windowSum += nums[right];
// shrink window on the left when violates target constraint
while (left < right && windowSum > target) {
windowSum -= nums[left];
left++;
}
if (windowSum == target) {
minWindowSize = Math.min(minWindowSize, right - left + 1);
}
}
return minWindowSize == Integer.MAX_VALUE ? INVALID_RESPONSE : minWindowSize;
}
}
If list contains negatives:
import java.util.Deque;
import java.util.ArrayDeque;
class Solution {
public int minSubArrayLen(int target, int[] nums) {
int n = nums.length;
long[] prefix = new long[n + 1];
for (int i = 0; i < n; i++) {
prefix[i + 1] = prefix[i] + nums[i];
}
Deque<Integer> deque = new ArrayDeque<>();
int minLen = Integer.MAX_VALUE;
for (int i = 0; i <= n; i++) {
// Try to shrink from the left
while (!deque.isEmpty() &&
prefix[i] - prefix[deque.peekFirst()] >= target) {
minLen = Math.min(minLen, i - deque.pollFirst());
}
// Maintain increasing prefix sums
while (!deque.isEmpty() &&
prefix[i] <= prefix[deque.peekLast()]) {
deque.pollLast();
}
deque.offerLast(i);
}
return minLen == Integer.MAX_VALUE ? 0 : minLen;
}
}
Longest Substring Without Repeating Characters
Given a string
s, find the length of the longest substring without duplicate characters.
Approach
- standard sliding window
- use set to track window validity (when advance, if set contains next right char, then advance left past the leftmost instance of that car, all intervening chars are uniqe)
Complexity
- Time complexity : O(2n)=O(n). In the worst case each character will be visited twice by i and j.
- Space complexity : O(min(m,n)). Same as the previous approach. We need O(k) space for the sliding window, where k is the size of the
Set. The size of the Set is upper bounded by the size of the string n and the size of the charset/alphabet m.
class Solution {
public int lengthOfLongestSubstring(String s) {
if (s == null || s.length() == 0) return 0;
// use to maintain window constrait (all unique)
Set<Character> windowSet = new HashSet<Character>();
int longestUniqueSubstring = Integer.MIN_VALUE;
int left = 0;
for (int right = 0; right < s.length(); right++) {
Character c = s.charAt(right);
if (windowSet.contains(c)) {
// window constraint violated, shrink
// advance to leftmost occurrence of c, advance past
while (left <= right) {
Character leftC = s.charAt(left++); //advance after access
windowSet.remove(leftC);
if (leftC.equals(c)) break;
}
}
windowSet.add(c);
longestUniqueSubstring = Math.max(longestUniqueSubstring, right - left + 1);
}
return longestUniqueSubstring;
}
}
Given two strings
sandtof lengthsmandnrespectively, return the minimum window substring ofssuch that every character int(including duplicates) is included in the window. If there is no such substring, return the empty string"".The testcases will be generated such that the answer is unique.
- Time Complexity : O(∣S∣+∣T∣) where |S| and |T| represent the lengths of strings S and T. The complexity is same as the previous approach. But in certain cases where ∣filtered_S∣ <<< ∣S∣, the complexity would reduce because the number of iterations would be 2∗∣filtered_S∣+∣S∣+∣T∣.
- Space Complexity : O(∣S∣+∣T∣).
class Solution {
public String minWindow(String s, String t) {
if (s.length() == 0 || t.length() == 0) {
return "";
}
// Dictionary which keeps a count of all the unique characters in t.
Map<Character, Integer> dictT = new HashMap<Character, Integer>();
for (int i = 0; i < t.length(); i++) {
int count = dictT.getOrDefault(t.charAt(i), 0);
dictT.put(t.charAt(i), count + 1);
}
// Number of unique characters in t, which need to be present in the desired window.
int required = dictT.size();
// Left and Right pointer
int l = 0, r = 0;
// formed is used to keep track of how many unique characters in t
// are present in the current window in its desired frequency.
// e.g. if t is "AABC" then the window must have two A's, one B and one C.
// Thus formed would be = 3 when all these conditions are met.
int formed = 0;
// Dictionary which keeps a count of all the unique characters in the current window.
Map<Character, Integer> windowCounts = new HashMap<
Character,
Integer
>();
// ans list of the form (window length, left, right)
int[] ans = { -1, 0, 0 };
while (r < s.length()) {
// Add one character from the right to the window
char c = s.charAt(r);
int count = windowCounts.getOrDefault(c, 0);
windowCounts.put(c, count + 1);
// If the frequency of the current character added equals to the
// desired count in t then increment the formed count by 1.
if (
dictT.containsKey(c) &&
windowCounts.get(c).intValue() == dictT.get(c).intValue()
) {
formed++;
}
// Try and contract the window till the point where it ceases to be 'desirable'.
while (l <= r && formed == required) {
c = s.charAt(l);
// Save the smallest window until now.
if (ans[0] == -1 || r - l + 1 < ans[0]) {
ans[0] = r - l + 1;
ans[1] = l;
ans[2] = r;
}
// The character at the position pointed by the
// `Left` pointer is no longer a part of the window.
windowCounts.put(c, windowCounts.get(c) - 1);
if (
dictT.containsKey(c) &&
windowCounts.get(c).intValue() < dictT.get(c).intValue()
) {
formed--;
}
// Move the left pointer ahead, this would help to look for a new window.
l++;
}
// Keep expanding the window once we are done contracting.
r++;
}
return ans[0] == -1 ? "" : s.substring(ans[1], ans[2] + 1);
}
}
HashMap
What it is
Map<K, V>stores key → value pairs- Keys are unique, values can repeat
Main Implementations
HashMap→ unordered, fastestLinkedHashMap→ insertion orderTreeMap→ sorted by key (BST)
Core Operations (Know by heart)
map.put(k, v); map.get(k); map.remove(k); map.containsKey(k); map.size();
Time Complexity
| Map | get / put / remove |
|---|---|
| HashMap | O(1) avg |
| LinkedHashMap | O(1) avg |
| TreeMap | O(log n) |
Iteration
for (Map.Entry<K,V> e : map.entrySet()) { }
for (K k : map.keySet()) { }
for (V v : map.values()) { }
Common Interview Methods
map.getOrDefault(k, 0); map.putIfAbsent(k, v); map.computeIfAbsent(k, k -> new ArrayList<>()); map.merge(k, 1, Integer::sum);
Frequency Count Pattern
map.merge(x, 1, Integer::sum);
Map of Lists Pattern
map.computeIfAbsent(k, x -> new ArrayList<>()).add(v);
Null Rules
HashMap→ 1 null key, many null valuesTreeMap→ ❌ null keysget()returnsnullif key missing
Critical Rules
- Keys must implement
equals()&hashCode() - Never modify map while iterating (unless using iterator)
When to Use Which
- Fast lookup →
HashMap - Preserve order →
LinkedHashMap - Sorted keys / range queries →
TreeMap
- Use a map to store the
compliment -> indexand return once you find it
class Solution {
public int[] twoSum(int[] nums, int target) {
//maps index of complement integers: complement -> index
Map<Integer, Integer> complimentIndexMap = new HashMap<Integer, Integer>();
for (int i = 0; i < nums.length; i++) {
int num = nums[i];
if (complimentIndexMap.containsKey(num)) {
return new int[]{complimentIndexMap.get(num), i};
}
int compliment = target - nums[i];
complimentIndexMap.put(compliment, i);
}
return null;
}
}
Linked Lists
Cycle In Linked List
- Could use “seen” hashset, O(n) time, O(n) space
- Improve with “Floyd’s Cycle Finding Algo”
- Two pointers, slow and fast. Fast moves two nodes at a time. If fast ever equals slow, then there is a cycle
- O(n), space O(1)
public class Solution {
public boolean hasCycle(ListNode head) {
if (head == null || head.next == null) {
return false;
}
ListNode follower = head, leader = head.next;
while(follower != leader) {
if (leader == null || leader.next == null) {
return false;
}
follower = follower.next;
leader = leader.next.next;
}
return true;
}
}
Deleting Sublists (e.g., all duplicates)
- Use a “sentinel” node – fake holder node to serve as virtual head of the list so that it can cover edge case where head of list is deleted
class Solution {
public ListNode deleteDuplicates(ListNode head) {
// virtual reference to head of list
ListNode sentinel = new ListNode(0, head);
// iterator
ListNode current = head;
// pointer to last unique node
ListNode lastUniqueNode = sentinel;
while (current != null) {
Integer currentVal = current.val;
if (current.next == null || current.next.val != currentVal) {
lastUniqueNode.next = current;
lastUniqueNode = current;
current = current.next;
} else {
// advance past all nodes of same value
current = advanceToNode(current, n -> n.val != currentVal);
// detect end of list
if (current == null) {
lastUniqueNode.next = current;
}
}
}
return sentinel.next;
}
/**
* Advance to first node that matches predicate or end of list
*/
private ListNode advanceToNode(ListNode current, Predicate<ListNode> predicate) {
while (current != null && !predicate.test(current)) {
current = current.next;
}
return current;
}
}
Rotation
- Rotating a list, best to calculate size first, then sanitize/normalize rotation by: rotation_value % list_size = normalized_rotation
- From this, identify the new tail node, which is: list_size – normalized_rotation – 1
- Then we need to make sure last node now points to old head, and we set next on the new tail to null
class Solution {
public ListNode rotateRight(ListNode head, int k) {
int length = findListLength(head);
if (length == 0) {
return head;
}
int rotate = k % length;
if (rotate == 0) {
return head;
}
int newEndIndex = length - rotate - 1;
int index = 0;
ListNode newTail = null, current = head, newHead = null;
while (true) {
// capture new tail node (need to nullify next)
if (index == newEndIndex) {
newTail = current;
} else if (index == newEndIndex + 1) {
newHead = current;
}
// connect old tail to old head and break out of look
if (current.next == null) {
current.next = head;
break;
}
current = current.next;
index++;
}
newTail.next = null;
return newHead;
}
private int findListLength(final ListNode head) {
ListNode current = head;
int size = 0;
while (current != null) {
current = current.next;
size++;
}
return size;
}
}
List Partitioning
- If asked to partition a list (e.g., around a pivot value, all nodes with val x appear before the nodes >= x, preserving order) then create a helper class for partition list, iterate through once, build the two partitions, merge and return (example).
class Solution {
class ListPartition {
ListNode head;
ListNode tail;
public ListPartition() {
this.head = null;
this.tail = null;
}
public ListPartition(ListNode head, ListNode tail) {
this.head = head;
this.tail = tail;
}
public void addNode(ListNode node) {
node.next = null;
if (this.head == null) {
this.head = node;
this.tail = node;
} else {
tail.next = node;
tail = node;
}
}
public ListNode mergeAsList(ListPartition toMerge) {
if (this.head == null) {
return toMerge.head;
} else if (toMerge.head == null) {
return this.head;
} else {
this.tail.next = toMerge.head;
return this.head;
}
}
}
public ListNode partition(ListNode head, int x) {
ListNode current = head, next = null;
ListPartition leftPartition = new ListPartition(), rightPartition = new ListPartition();
while (current != null) {
next = current.next;
if (current.val < x) {
leftPartition.addNode(current);
} else {
rightPartition.addNode(current);
}
current = next;
}
return leftPartition.mergeAsList(rightPartition);
}
}
Removing Nth Node from **END** of list
- use two pointers: leader, follower: distance of N+1 (note: this points to node before one we want to delete, so we can do
current = current.next.nexteasily) apart (only start increase follower pointer once leader pointer is N steps ahead). - Then, when follower reaches end, can delete Node at follower
class Solution {
public ListNode removeNthFromEnd(ListNode head, int n) {
ListNode dummy = new ListNode(0);
dummy.next = head;
ListNode first = dummy;
ListNode second = dummy;
// Advances first pointer so that the gap between first and second is n nodes apart
for (int i = 1; i <= n + 1; i++) {
first = first.next;
}
// Move first to the end, maintaining the gap
while (first != null) {
first = first.next;
second = second.next;
}
second.next = second.next.next;
return dummy.next;
}
}
LRU Cache
- Defined here
- Implement with
- HashMap and Doubly Linked list
- Use Node to store values in both linked list and hashmap (class that contains key, value, next, prev)
- use size of hashmap to track size
- add to end of list
- if size grows to capacity remove head and remove from map
- be careful when updating a value that already exists – end state needs to be node at end of list and node has updated value
- be careful when removing values – consider
- Empty list, removing tail, removing head, removing tail
- consider using sentinel nodes for head and tail
class LRUCache {
class CacheNode<K,V> {
public CacheNode(K key, V val) {
this.prev = null;
this.next = null;
this.val = val;
this.key = key;
}
CacheNode prev;
CacheNode next;
V val;
K key;
}
// max capacity of the cache
private final int capacity;
private final Map<Integer, CacheNode<Integer, Integer>> cacheMap;
private CacheNode<Integer, Integer> cacheListHead, cacheListTail;
public LRUCache(int capacity) {
this.capacity = capacity;
this.cacheListHead = null;
this.cacheListTail = null;
this.cacheMap = new HashMap<Integer, CacheNode<Integer, Integer>>(capacity);
}
public int get(int key) {
if (this.cacheMap.containsKey(key)) {
CacheNode<Integer, Integer> node = cacheMap.get(key);
refreshNode(node);
return node.val;
}
return -1;
}
public void put(int key, int val) {
CacheNode<Integer, Integer> newNode = new CacheNode(key, val);
if (this.cacheMap.containsKey(key)) {
removeCacheListNode(this.cacheMap.get(key));
this.cacheMap.remove(key);
} else {
evictLruIfRequired();
}
this.cacheMap.put(key, newNode);
appendCacheListNode(newNode);
}
private void refreshNode(CacheNode<Integer, Integer> node) {
removeCacheListNode(node);
appendCacheListNode(node);
}
private void evictLruIfRequired() {
if (this.cacheMap.size() == capacity) {
cacheMap.remove(this.cacheListHead.key);
removeCacheListNode(this.cacheListHead);
}
}
private void appendCacheListNode(CacheNode<Integer, Integer> newNode) {
if (this.cacheListHead == null) {
this.cacheListHead = newNode;
this.cacheListTail = newNode;
} else {
this.cacheListTail.next = newNode;
newNode.prev = this.cacheListTail;
this.cacheListTail = newNode;
}
}
private void removeCacheListNode(CacheNode<Integer, Integer> node) {
if (node == this.cacheListHead && node == this.cacheListTail) {
this.cacheListHead = null;
this.cacheListTail = null;
} else if (node == this.cacheListHead) {
// remove head
this.cacheListHead = this.cacheListHead.next;
this.cacheListHead.prev = null;
} else if (node == this.cacheListTail) {
// remove tail
this.cacheListTail = this.cacheListTail.prev;
this.cacheListTail.next = null;
} else {
// remove middle
node.prev.next = node.next;
node.next.prev = node.prev;
}
}
}
Lessons Learned
- When modifying the list, if chance of deleting head node, use “sentinel”
- 2 pointers for loop detection, one travers 2x faster than other. If they ever point to same node, then loop.
class Solution {
public ListNode mergeTwoLists(ListNode list1, ListNode list2) {
ListNode sentinel = new ListNode(0);
ListNode tail = sentinel;
while (list1 != null && list2 != null) {
if (list1.val < list2.val) {
tail.next = list1;
tail = tail.next;
list1 = list1.next;
} else {
tail.next = list2;
tail = tail.next;
list2 = list2.next;
}
}
if (list1 == null) {
tail.next = list2;
} else {
tail.next = list1;
}
return sentinel.next;
}
}
Stacks
Validating Matching Parentheses
- Push opening parens, when encounter closing, pop and make sure
- Have a map of closing -> opening parens for look up
- Remember to check edge cases (all closing, all opening) – do this by implementing careful checks of size of stack, and remember to check size of stack at end to ensure it equals 0, otherwise there’s something left over
Min Stack
Goal: Support push, pop, top, and getMin in O(1) time.
- Idea: Use one main stack for values and a second stack to track current minimums.
- Push rule: Push
xonto min-stack ifx <= currentMin(handles duplicates). - Pop rule: If
top(main) == top(min), pop both stacks. - Note – I used a wrapper class (
Node {int val}) for this, so I can identify when I’m popping a node from main stack that needs to be popped from other stack. If not doing this (for slight space improvement), then need to add int to minStack whenever new int value is <= value on top of minStack
class MinStack {
private class Node {
int val;
public Node(int val) {
this.val = val;
}
private boolean lessThanOrEqual(Node other) {
return this.val <= other.val;
}
}
private static Stack<Node> stack;
private static Stack<Node> minStack;
public MinStack() {
this.stack = new Stack<Node>();
this.minStack = new Stack<Node>();
}
public void push(int val) {
Node newNode = new Node(val);
stack.push(newNode);
if (minStack.size() == 0 || newNode.lessThanOrEqual(minStack.peek())) {
minStack.push(newNode);
}
}
public void pop() {
if (stack.pop() == minStack.peek()) {
minStack.pop();
}
}
public int top() {
return stack.peek().val;
}
public int getMin() {
return minStack.peek().val;
}
}
Operations:
top(): peek main stack.getMin(): peek min stack.push()andpop(): maintain min stack accordingly.
Complexity:
- Time: O(1) per operation
- Space: O(n) (extra stack for min values)
Reverse Polish Notation
- Defined here
- Array of operands and operations (“4”, “5”, “+”)
- Maintain a stack for operands
- Traverse list, when operand (or not operation char), push to stack. When encounter operator, pop twice from stack (
rightOperand, thenleftOperand) and execute operation – push result back to stack
class Solution {
private static final Set<String> OPERATORS = Set.of("+", "-", "/", "*");
public int evalRPN(String[] tokens) {
Stack<Integer> operands = new Stack<Integer>();
for (String token : tokens) {
if (OPERATORS.contains(token)) {
Integer rightOperand = operands.pop(),
leftOperand = operands.pop();
switch (token) {
case "+":
operands.push(leftOperand + rightOperand);
break;
case "-":
operands.push(leftOperand - rightOperand);
break;
case "/":
operands.push(leftOperand / rightOperand);
break;
case "*":
operands.push(leftOperand * rightOperand);
break;
}
} else {
operands.push(Integer.parseInt(token));
}
}
return operands.pop();
}
}
Intervals
Note
- When dealing with intervals be careful checking or overlap – need to check if second interval starts in, ends in, or completely overlaps interval 1 – also check if interval 2 completely encapsulates interval 1!!
private boolean intervalOverlaps(final int[] left, final int[] right) {
if ( (right[0] <= left[0] && left[0] <= right[1])
|| (right[0] <= left[1] && left[1] <= right[1])
|| (left[0] <= right[0] && right[0] <= left[1])
|| (left[0] <= right[1] && right[1] <= left[1])) {
return true;
}
return false;
}
Merge Intervals
- Merge things like
[start,end]([1,3], [2,5]=>[1,5])- Sort, then iterate through (for loop, embed while loop to push
ialong all overlapping intervals), merge as you go and add to new answer list - caution: (
[1,10], [2,5]=>[1,10]) – don’t forget case where left interval consumes all of a subsequent interval O(n log n)(the sorting dominates the complexity analysis)- Handy: documentation
List<int[]> ans = new ArrayList<int[]>();int[][] primAns = ans.toArray(new int[ans.size()][]);
- Sort, then iterate through (for loop, embed while loop to push
class Solution {
public int[][] merge(int[][] intervals) {
// sort array based on start time
Arrays.sort(intervals, (a, b) -> Integer.compare(a[0], b[0]));
List<int[]> ans = new ArrayList<int[]>();
for (int i = 0; i < intervals.length; i++) {
int merged_interval_start = intervals[i][0];
int left_end = intervals[i][1];
// advance
while(i + 1 < intervals.length && left_end >= intervals[i+1][0]) {
i++;
left_end = Math.max(left_end, intervals[i][1]);
}
ans.add(new int[] {merged_interval_start, left_end});
}
int[][] primAns = ans.toArray(new int[ans.size()][]);
return primAns;
}
}
Insert Interval
- Sort list of intervals
- Iterate through and have 2 branch if: 1st check if overlaps, then merge and consider if it also overlaps subsequent intervals too OR 2 check if it is before the current interval, in which case simply add. Make sure to check if should be just added to the end.
class Solution {
public int[][] insert(int[][] intervals, int[] newInterval) {
List<int[]> ans = new ArrayList<int[]>();
boolean inserted = false;
for (int i = 0; i<intervals.length; i++) {
if (!inserted && intervalOverlaps(intervals[i], newInterval)) {
int mergedStart = Math.min(intervals[i][0], newInterval[0]);
int mergedEnd = Math.max(intervals[i][1], newInterval[1]);
// interval overlaps, merge this and all subsequent overlapping intervals
while (i+1 < intervals.length && intervalOverlaps(intervals[i+1], newInterval)) {
i++;
mergedEnd = Math.max(intervals[i][1], mergedEnd);
}
ans.add(new int[] { mergedStart, mergedEnd });
inserted = true;
continue; // don't re-add merged interval
} else if (!inserted && newInterval[0] < intervals[i][0]) {
inserted = true;
ans.add(newInterval);
}
ans.add(intervals[i]);
}
if (!inserted) {
ans.add(newInterval);
}
int[][] primAns = ans.toArray(new int[ans.size()][]);
return primAns;
}
private boolean intervalOverlaps(final int[] left, final int[] right) {
if ( (right[0] <= left[0] && left[0] <= right[1])
|| (right[0] <= left[1] && left[1] <= right[1])
|| (left[0] <= right[0] && right[0] <= left[1])
|| (left[0] <= right[1] && right[1] <= left[1])) {
return true;
}
return false;
}
}
Min Arrows to Burst Balloons – Greed Overlap
- Problem
- Approach:
- sort intervals, traverse through and every time you encounter an interval that doesn’t overlap with all previous (i.e, it’s start time is after the end of the first interval) then increment the count and move onto the next one
- NOTE: sort by
endof the interval:
If we sort by start point and shoot as far right as possible, we'll shoot too far right for balloon 2 :
| | (1)
| | (2)
| | (3)
^
Sort by end point and shoot as far right as possible and we'll get the correct answer which is two arrows:
| | (2)
| | (1)
| | (3)
^ ^
You could also sort by start position in decreasing order and apply the same logic by shooting as far left as possible.class Solution {
public int findMinArrowShots(int[][] points) {
// sort intervals by x_start
Arrays.sort(points, (a, b) -> Integer.compare(a[1], b[1]));
int numArrows = 0;
for (int i = 0; i < points.length; i++) {
int x_start = points[i][0];
int x_end = points[i][1];
while (i+1 < points.length && points[i+1][0] <= x_end) {
i++;
}
numArrows++;
}
return numArrows;
}
}
Binary Trees
- Definition: A binary tree where for every node
left subtree < node < right subtree - In-order traversal: Visits nodes in sorted order
- Search / Insert / Delete:
- Average:
O(log n) - Worst (skewed):
O(n)
- Average:
- Common operations: search, insert, delete, find min/max, predecessor/successor
- Key property: All values in left subtree are smaller; all in right are larger (recursively)
- Deletion cases:
- Leaf → remove directly
- One child → replace with child
- Two children → replace with inorder successor/predecessor
- Validation pattern: Use value bounds (
min < node.val < max), not just parent comparison - Balanced BSTs: (AVL, Red-Black) keep height
O(log n) - Use cases: ordered data, range queries, TreeMap/TreeSet internals
Interview takeaway:
In-order traversal = sorted data; performance depends on tree balance.
Build tree from inorder and preorder lists
- Key point:
- use the preorder list as list of root nodes, iterate through these
- at same time, use inorder list to identify nodes that are to left and right of the current root node (get index of current root in inorder list, then all nodes to left are in left subtree, and same with right)
- recursively traverse to smaller and smaller sublists this way (startIdx, endIdx) and when startIdx > endIdx, return null.
- Note: if given the inorder and postorder, works exact same just backwards:
- start at end of postorder and iterate backwards for each new root node
- traverse right subtrees first
inorder + preorder
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
private int[] preorder;
private int[] inorder;
private Map<Integer, Integer> inOrderIdxMap;
private int preIdx;
public TreeNode buildTree(int[] preorder, int[] inorder) {
if (preorder.length == 0) {
return null;
}
this.preorder = preorder;
this.inorder = inorder;
this.inOrderIdxMap = computeReverseIdxMap(inorder);
this.preIdx = 0;
return computeTree(0, preorder.length-1);
}
private TreeNode computeTree(int subStartIdx, int subEndIdx) {
if (subStartIdx > subEndIdx) {
return null;
}
int val = preorder[preIdx];
TreeNode root = new TreeNode(val);
preIdx++;
root.left = computeTree(subStartIdx, inOrderIdxMap.get(val) - 1);
root.right = computeTree(inOrderIdxMap.get(val)+1, subEndIdx);
return root;
}
private Map<Integer, Integer> computeReverseIdxMap(int[] arr) {
Map<Integer, Integer> idxMap = new HashMap<Integer, Integer>();
for(int i = 0; i<arr.length; i++) {
idxMap.put(arr[i], i);
}
return idxMap;
}
}
inorder + postorder
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
Map<Integer, Integer> inorderReverseIdx;
int postOrderIdx;
public TreeNode buildTree(int[] inorder, int[] postorder) {
if (postorder.length == 0) {
return null;
}
inorderReverseIdx = computeArrayReverseIdx(inorder);
postOrderIdx = postorder.length - 1;
return computeTree(postorder, 0, postOrderIdx);
}
private TreeNode computeTree(int[] postorder, int startIdx, int endIdx) {
if (startIdx > endIdx) {
return null;
}
int nodeVal = postorder[postOrderIdx--];
TreeNode node = new TreeNode(nodeVal);
int nodeValOrderIdx = inorderReverseIdx.get(nodeVal);
node.right = computeTree(postorder, nodeValOrderIdx+1, endIdx);
node.left = computeTree(postorder, startIdx, nodeValOrderIdx-1);
return node;
}
private Map<Integer, Integer> computeArrayReverseIdx(int[] arr) {
Map<Integer, Integer> reverseMap = new HashMap<>();
for(int i = 0; i < arr.length; i++) {
reverseMap.put(arr[i], i);
}
return reverseMap;
}
}
Flatten BT into linked list (node.right only) using pre-order
- Trick: traverse using preorder, add to queue, then iterate queue, nulling node.left, and daisy-chaining node.right
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
Queue<TreeNode> treeNodeQueue;
public void flatten(TreeNode root) {
if (root == null) {
return;
}
treeNodeQueue = new LinkedList<>();
computeFlatQueue(root);
TreeNode prev = null;
while(!treeNodeQueue.isEmpty()) {
TreeNode current = treeNodeQueue.poll();
current.left = null;
if (prev != null) {
prev.right = current;
}
prev = current;
}
}
private void computeFlatQueue(TreeNode node) {
if (node == null) {
return;
}
//pre-order traversal
treeNodeQueue.offer(node);
computeFlatQueue(node.left);
computeFlatQueue(node.right);
}
}
BST Iterator
- Two Approaches
- inorder traverse and build a queue / list of inorder array, store pointer, advance for each next() call
- build a custom recursion stack
flattening inorder traversal
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class BSTIterator {
private Queue<Integer> treeValueQueue;
public BSTIterator(TreeNode root) {
treeValueQueue = new LinkedList<Integer>();
computeInOrderValueQueue(root);
}
public int next() {
if (hasNext()) {
return treeValueQueue.poll();
}
return -1; // throw exception
}
public boolean hasNext() {
return !treeValueQueue.isEmpty();
}
private void computeInOrderValueQueue(TreeNode node) {
if (node == null) {
return;
}
computeInOrderValueQueue(node.left);
treeValueQueue.offer(node.val);
computeInOrderValueQueue(node.right);
}
}
/**
* Your BSTIterator object will be instantiated and called as such:
* BSTIterator obj = new BSTIterator(root);
* int param_1 = obj.next();
* boolean param_2 = obj.hasNext();
*/
controlled recursion
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class BSTIterator {
private Stack<TreeNode> recursionStack;
public BSTIterator(TreeNode root) {
recursionStack = new Stack<>();
diveLeftSubTrees(root);
}
private void diveLeftSubTrees(TreeNode node) {
if (node == null) {
return;
}
recursionStack.push(node);
diveLeftSubTrees(node.left);
}
public int next() {
// throw exception if no next
TreeNode node = recursionStack.pop();
diveLeftSubTrees(node.right);
return node.val;
}
public boolean hasNext() {
if (recursionStack.isEmpty()) {
return false;
}
return true;
}
}
/**
* Your BSTIterator object will be instantiated and called as such:
* BSTIterator obj = new BSTIterator(root);
* int param_1 = obj.next();
* boolean param_2 = obj.hasNext();
*/
Lowest Common Ancestor
class Solution {
private TreeNode ans;
public Solution() {
// Variable to store LCA node.
this.ans = null;
}
private boolean recurseTree(TreeNode currentNode, TreeNode p, TreeNode q) {
// If reached the end of a branch, return false.
if (currentNode == null) {
return false;
}
// Left Recursion. If left recursion returns true, set left = 1 else 0
int left = this.recurseTree(currentNode.left, p, q) ? 1 : 0;
// Right Recursion
int right = this.recurseTree(currentNode.right, p, q) ? 1 : 0;
// If the current node is one of p or q
int mid = (currentNode == p || currentNode == q) ? 1 : 0;
// If any two of the flags left, right or mid become True
if (mid + left + right >= 2) {
this.ans = currentNode;
}
// Return true if any one of the three bool values is True.
return (mid + left + right > 0);
}
public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
// Traverse the tree
this.recurseTree(root, p, q);
return this.ans;
}
}
Rightside view
- Return list of nodes visible from right in a binary tree
- Solution:
- post-order traversal (rightmost first), carry a level int, add new levels to map (level -> node) unless already exist
- because rightfirst traversal, the rightmost nodes will be added
- optimisation: can just add to answer list directly, don’t need map, add to list if current level > current size of answer list.
BT Level Order Traversal (Each Row)
Lesson Learned:
- Instead of storing a pair/wrapped node in the queue, look at the internal for loop
Solution:
- BFS – build answer as progress through the BT
- Alternative: can do it recursively, preorder traversal, carrying level offset through recursion
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
public List<List<Integer>> levelOrder(TreeNode root) {
List<List<Integer>> answer = new ArrayList<>();
if (root == null) {
return answer;
}
Queue<TreeNode> processingQueue = new LinkedList<TreeNode>();
processingQueue.offer(root);
int level = 0;
while (!processingQueue.isEmpty()) {
answer.add(new ArrayList<>());
int levelWidth = processingQueue.size();
for (int i = 0; i < levelWidth; i++) {
TreeNode node = processingQueue.remove();
answer.get(level).add(node.val);
if (node.left != null) processingQueue.offer(node.left);
if (node.right != null) processingQueue.offer(node.right);
}
level++;
}
return answer;
}
}
Insert into BST
class Solution {
public TreeNode insertIntoBST(TreeNode root, int val) {
if (root == null) return new TreeNode(val);
if (val > root.val) root.right = insertIntoBST(root.right, val);
if (val < root.val) root.left = insertIntoBST(root.left, val);
return root;
}
}
Delete Element from BST
NOTE:
- The trick here is to remember how ordering works – see successor and predecessor implementation
- Then algo is:
- if in right ST, set
node.right = delete(node.right), i.e., recurse right - else if in left ST, set
node.left = delete(node.left), i.e., recurse left - else this is the node we want to delete, 3 scenarios:
- left & right children are null, return null
- [right preference] if right child not null, replace current with successor, then set
node.rightto node returned when deleting that new node from right subtree (recurse) - if right child is null, then left must not be null, replace current with predecessor, then set
node.leftto node returned when deleting that new node from left subtree
- if in right ST, set
- Complexity:
O(H1+H2)=O(H), where H1 = search for node to delete and H2 = search for replacement predecessor/successor
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
public TreeNode deleteNode(TreeNode root, int key) {
if (root == null) return null;
if (key > root.val) {
root.right = deleteNode(root.right, key);
} else if (key < root.val) {
root.left = deleteNode(root.left, key);
} else {
if (root.left == null && root.right == null) {
return null;
} else if (root.right != null) {
root.val = successor(root).val;
root.right = deleteNode(root.right, root.val);
} else {
root.val = predecessor(root).val;
root.left = deleteNode(root.left, root.val);
}
}
return root;
}
private TreeNode successor(TreeNode node) {
node = node.right;
while (node.left != null) node = node.left;
return node;
}
private TreeNode predecessor(TreeNode node) {
node = node.left;
while (node.right != null) node = node.right;
return node;
}
}
Valid BST
- Just recurse and carry the upper/lower limits
class Solution {
public boolean isValidBST(TreeNode root) {
return performIsValidBST(root, Long.MIN_VALUE, Long.MAX_VALUE);
}
private boolean performIsValidBST(TreeNode node, long min, long max) {
if (node == null) {
return true;
}
if (node.val <= min || node.val >= max ) {
return false;
}
if (!performIsValidBST(node.left, min, node.val)) return false;
if (!performIsValidBST(node.right, node.val, max)) return false;
return true;
}
}
Approach:
- create list by inorder traversal
- then kind of perform binary search patter, new root is midpoint, recurse for left and right subtrees
gotchas:
- end comparison:
left>right - left and right should always point to valid indices, so start with
inorderList.size()-1
Complexity
- time: O(n)
- compute in order list: O(n)
- build tree O(n)
- O(n+n) => O(n)
- Space (recursion stack): O(n) worse case for severely unbalanced tree
- inorder traversal O(n) in worse case
- building tree O(log n)
- => O(n)
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
public TreeNode balanceBST(TreeNode root) {
if (root == null) return root;
List<TreeNode> inOrderList = new ArrayList<TreeNode>();
calculateInOrderList(root, inOrderList);
return createBinaryTree(inOrderList, 0, inOrderList.size()-1);
}
private TreeNode createBinaryTree(List<TreeNode> inOrderList, int left, int right) {
if (left > right) return null;
int mid = left + (right - left) / 2;
TreeNode root = inOrderList.get(mid);
root.left = createBinaryTree(inOrderList, left, mid-1);
root.right = createBinaryTree(inOrderList, mid+1, right);
return root;
}
private void calculateInOrderList(TreeNode root, List<TreeNode> inOrderList) {
if (root == null) return;
calculateInOrderList(root.left, inOrderList);
inOrderList.add(root);
calculateInOrderList(root.right, inOrderList);
}
}
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
public boolean isBalanced(TreeNode root) {
if (root == null || (root.left == null && root.right == null))
return true;
return checkBtIsBalanced(root) != -1;
}
public int checkBtIsBalanced(TreeNode root) {
if (root == null) return 0;
int left = checkBtIsBalanced(root.left);
if (left == -1) return -1;
int right = checkBtIsBalanced(root.right);
if (right == -1) return -1;
int differenceInHeight = Math.abs(left-right);
if (differenceInHeight > 1)
return -1;
return 1 + Math.max(right, left);
}
}
Graphs
Capture Area
- grid of Xs and Os, replace Os with Xs if Xs completely surrounding the Os (Os can “escape” if touch the edges)
Naive solution
class Solution {
private static final Character REGION_CHAR = 'O';
private static final Character SURROUND_CHAR = 'X';
record CoOrd(int r, int c) {
public CoOrd applyOffset(final CoOrd coOrd) {
return new CoOrd(r() + coOrd.r(), c() + coOrd.c());
}
};
// search directions
private static final List<CoOrd> directions = new ArrayList<CoOrd>(List.of(
new CoOrd(0,1), // right
new CoOrd(1,0), // down
new CoOrd(0, -1), // left
new CoOrd(-1, 0) // up
));
Set<CoOrd> visited;
public void solve(char[][] board) {
visited = new HashSet<CoOrd>();
if (board.length == 0) {
return;
}
for (int r = 0; r < board.length; r++) {
for (int c = 0; c < board[0].length; c++) {
CoOrd coOrd = new CoOrd(r, c);
if (visited.contains(coOrd)) continue;
if (board[r][c] == REGION_CHAR) {
attemptToCapture(board, coOrd);
} else {
visited.add(coOrd);
}
}
}
}
/**
* Explores a "potential" region on a board given a starting point.
* If the startCoOrd is a cell of a larger region (region is "O"s surrounded by "X"s),
* then it **mutates** the board by replacing all "O"s with "X"s
*
* BFS - need to be ensure all connected "O" cells are actually a region
*
* returns boolean true if captured a region, false otherwise
*/
private boolean attemptToCapture(char[][] board, CoOrd startCoOrd) {
// assumptions - startCoOrd points to "O" within board
// board only contains "O"s and "X"s
if (board.length == 0) return false;
final int minR = 0, maxR = board.length;
final int minC = 0, maxC = board[0].length;
List<CoOrd> regionCells = new LinkedList<CoOrd>();
Queue<CoOrd> queue = new LinkedList<CoOrd>();
boolean validRegion = true;
queue.offer(startCoOrd);
while(!queue.isEmpty()) {
CoOrd currentCoOrd = queue.poll();
visited.add(currentCoOrd);
char currentVal = board[currentCoOrd.r()][currentCoOrd.c()];
if (currentVal != REGION_CHAR) continue;
// abandon if REGION_CHAR on edge of board
if (currentCoOrd.r() <= minR || currentCoOrd.r() >= maxR - 1
|| currentCoOrd.c() <= minC || currentCoOrd.c() >= maxC - 1) {
validRegion = false;
}
regionCells.add(currentCoOrd);
for (CoOrd dir : directions) {
CoOrd nextCell = currentCoOrd.applyOffset(dir);
if (nextCell.r() < minR || nextCell.r() >= maxR
|| nextCell.c() < minC || nextCell.c() >= maxC) {
// ran over edge of board
continue;
}
// already visited
if (visited.contains(nextCell)) continue;
queue.offer(nextCell);
}
}
// replace region cells
if (validRegion) {
regionCells.forEach(c -> board[c.r()][c.c()] = SURROUND_CHAR);
}
return true;
}
}
Slightly more efficient:
- Iterate over board’s edges, identify “O”s at the edge, DFS/BFS from this point marking them as “S” (safe)
- Then iterate over every node again swapping: S -> O, O -> X, X -> X (no op)
class Solution {
private static final Character REGION_CHAR = 'O';
private static final Character SURROUND_CHAR = 'X';
private static final Character SAFE_CHAR = 'S';
record CoOrd(int r, int c) {
public CoOrd applyOffset(final CoOrd coOrd) {
return new CoOrd(r() + coOrd.r(), c() + coOrd.c());
}
};
// search directions
private static final List<CoOrd> directions = new ArrayList<CoOrd>(List.of(
new CoOrd(0,1), // right
new CoOrd(1,0), // down
new CoOrd(0, -1), // left
new CoOrd(-1, 0) // up
));
Set<CoOrd> visited;
int maxR, maxC;
public void solve(char[][] board) {
visited = new HashSet<CoOrd>();
if (board.length == 0) {
return;
}
maxR = board.length;
maxC = board[0].length;
for (int r = 0; r < maxR; r++) {
CoOrd leftCell = new CoOrd(r, 0), rightCell = new CoOrd(r, maxC - 1);
if (board[leftCell.r()][leftCell.c()] == REGION_CHAR) markSafe(board, leftCell);
if (board[rightCell.r()][rightCell.c()] == REGION_CHAR) markSafe(board, rightCell);
}
for (int c = 0; c < maxC; c++) {
CoOrd topCell = new CoOrd(0, c), bottomCell = new CoOrd(maxR - 1, c);
if (board[topCell.r()][topCell.c()] == REGION_CHAR) markSafe(board, topCell);
if (board[bottomCell.r()][bottomCell.c()] == REGION_CHAR) markSafe(board, bottomCell);
}
for (int r = 0; r < maxR; r++) {
for (int c = 0; c < maxC; c++) {
if (board[r][c] == SAFE_CHAR) {
board[r][c] = REGION_CHAR;
} else if (board[r][c] == REGION_CHAR) {
board[r][c] = SURROUND_CHAR;
}
}
}
}
private void markSafe(char[][] board, CoOrd cell) {
if (board[cell.r()][cell.c()] != REGION_CHAR) return;
board[cell.r()][cell.c()] = SAFE_CHAR;
directions.forEach( dir -> {
CoOrd nextCell = dir.applyOffset(cell);
if (nextCell.r() >= 0 && nextCell.r() < maxR
&& nextCell.c() >=0 && nextCell.c() < maxC) {
markSafe(board, nextCell);
}
});
}
}
Path Exist in Graph between Node A and B (acyclic undirected)
- given adjacency list an start, end
- algo:
- need to prepare adjacency list for lookups, transform to a map (or simple list) – note/important remember to add backlinks for undirected graphs (i.e., if node 0 connected to node 1, then node 1 is also connected to node 0, this needs to be captured in the edge representation)
- Then do bfs from start node, check if you arrive at the end node
- time complexity: O(V+E) – vertices, edges
- need to iterate over all edges to create adjacency list
- in while loop visit each vertex once
- in the for loop inside the while, will visit at most E iterations
- space: O(V+E)
- adjacency list will contain O(V+E) elements
- queue will contain O(V) elements
- seen will contain O(V) space to store visited nodes
class Solution {
public boolean validPath(int n, int[][] edges, int start, int end) {
List<List<Integer>> adjacency_list = new ArrayList<>();
for (int i = 0; i < n; i++) {
adjacency_list.add(new ArrayList<>());
}
for (int[] edge : edges) {
adjacency_list.get(edge[0]).add(edge[1]);
adjacency_list.get(edge[1]).add(edge[0]);
}
Queue<Integer> queue = new LinkedList<>();
queue.add(start);
boolean seen[] = new boolean[n];
Arrays.fill(seen, false);
seen[start] = true;
while (!queue.isEmpty()) {
// Get the current node.
int node = queue.poll();
// Check if we have reached the target node.
if (node == end) {
return true;
}
// Add all neighbors to the stack.
for (int neighbor : adjacency_list.get(node)) {
// Check if neighbor has been added to the queue before.
if (!seen[neighbor]) {
seen[neighbor] = true;
queue.add(neighbor);
}
}
}
return false;
}
}
Find all paths between A and B
- The processing queue stores paths (list of nodes) that you process, pop, check last, add each new path (all the nodes last will go to), when you’re finished return the list
class Solution {
public List<List<Integer>> allPathsSourceTarget(int[][] graph) {
int numGraphNodes = graph.length;
List<List<Integer>> pathsToTarget = new LinkedList<>();
Queue<LinkedList<Integer>> processingQueue = new ArrayDeque<>();
processingQueue.offer(new LinkedList<Integer>(List.of(0)));
while (!processingQueue.isEmpty()) {
LinkedList<Integer> currentPath = processingQueue.poll();
int pathTailNode = currentPath.peekLast();
if (pathTailNode == numGraphNodes - 1) {
pathsToTarget.add(currentPath);
} else {
for (int nextNode : graph[pathTailNode]) {
LinkedList<Integer> newPath = new LinkedList<>(currentPath);
newPath.add(nextNode);
processingQueue.offer(newPath);
}
}
}
return pathsToTarget;
}
}
Set Next Nodes across levels in BST
- Trick: remember that levels are added level per level, so you can have an inner loop to iterate over all nodes at a given level
/*
// Definition for a Node.
class Node {
public int val;
public Node left;
public Node right;
public Node next;
public Node() {}
public Node(int _val) {
val = _val;
}
public Node(int _val, Node _left, Node _right, Node _next) {
val = _val;
left = _left;
right = _right;
next = _next;
}
};
*/
class Solution {
public Node connect(Node root) {
if (root == null) return root;
Queue<Node> processingQueue = new ArrayDeque<>();
processingQueue.offer(root);
while (!processingQueue.isEmpty()) {
int levelWidth = processingQueue.size();
Node prev = null;
for (int i = 0; i < levelWidth; i++) {
Node currentNode = processingQueue.poll();
// reset the pointer
currentNode.next = null;
if (prev != null)
prev.next = currentNode;
if (currentNode.left != null) processingQueue.offer(currentNode.left);
if (currentNode.right != null) processingQueue.offer(currentNode.right);
prev = currentNode;
}
}
return root;
}
}
Shortest Path on a Map
- BFS
- Trick: note, must process each level in turn, see when we increment the distance count. If incremented after each element polled from queue in outer loop would be incorrect
- could also overwrite input to keep track of distance AND visited
- store the distance on the queue too
class Solution {
private record Cell(int r, int c) {
/**
* Adds two cells together TODO
*/
public Cell applyOffset(final Cell other) {
return new Cell(this.r() + other.r(), this.c() + other.c());
}
};
// Search directions
private static final List<Cell> SEARCH_DIRS = new ArrayList<Cell>(List.of(
new Cell(-1,0), // up
new Cell(-1,1), // up, right
new Cell(0,1), // right
new Cell(1,1), // down, right
new Cell(1,0), // down
new Cell(1,-1), // down, left
new Cell(0,-1), // left
new Cell(-1,-1) // up, left
));
public int shortestPathBinaryMatrix(int[][] grid) {
int gridSize = grid.length;
if (gridSize == 0 || grid[0][0] != 0 || grid[gridSize-1][gridSize-1] != 0) return -1;
// TODO assert n == m
Cell startCell = new Cell(0, 0);
Cell endCell = new Cell(gridSize - 1, gridSize - 1);
Queue<Cell> processingQueue = new ArrayDeque<>();
processingQueue.offer(startCell);
Set<Cell> visited = new HashSet<>();
int pathLength = 1;
while (!processingQueue.isEmpty()) {
int levelWidth = processingQueue.size();
for (int i = 0; i < levelWidth; i++) {
Cell currentCell = processingQueue.poll();
if (currentCell.equals(endCell)) return pathLength;
visited.add(currentCell);
for (Cell dir : SEARCH_DIRS) {
Cell nextCell = dir.applyOffset(currentCell);
if (visited.contains(nextCell)) continue;
if (nextCell.r() >= 0 && nextCell.r() < gridSize
&& nextCell.c() >= 0 && nextCell.c() < gridSize
&& grid[nextCell.r()][nextCell.c()] == 0) {
processingQueue.offer(nextCell);
}
}
}
pathLength++;
}
return -1;
}
}
N-Ary Tree Level Order Traversal
/*
// Definition for a Node.
class Node {
public int val;
public List<Node> children;
public Node() {}
public Node(int _val) {
val = _val;
}
public Node(int _val, List<Node> _children) {
val = _val;
children = _children;
}
};
*/
class Solution {
public List<List<Integer>> levelOrder(Node root) {
List<List<Integer>> res = new LinkedList<>();
if (root == null) return res;
Queue<Node> processingQueue = new LinkedList<>();
processingQueue.offer(root);
while (!processingQueue.isEmpty()) {
int levelWidth = processingQueue.size();
List<Integer> levelList = new ArrayList<>();
for (int i = 0; i < levelWidth; i++) {
Node node = processingQueue.poll();
levelList.add(node.val);
node.children.stream().filter(Objects::nonNull).forEach(processingQueue::offer);
}
res.add(levelList);
}
return res;
}
}
Spreading Disease – rotting oranges
- matrix of empty space, fresh oranges, or rotten oranges, how many ticks before all infects:
- Algo:
- trick: build starting processing queue containing all starting rotten oranges AND while doing this count how many fresh oranges there are
- if no fresh oranges before starting, return 0
- then perform BFS (doe the queue size trick to increment tick after each “level”)
- mark in place!
- NOTE – IMPORTANT – “BFS INFECTION” mark the orange as rotten when adding to the processing queue, not when visiting (prevents other adjacent infected orange from re-adding and decrementing fresh oranges more than once)
class Solution {
private static final int ROTTON_ORANGE = 2;
private static final int FRESH_ORANGE = 1;
private static final int EMPTY = 0;
private static final int IMPOSSIBLE_VAL = -1;
private record Cell(int r, int c) {
public Cell applyOffset(Cell other) {
return new Cell(this.r() + other.r(), this.c() + other.c());
}
};
private final List<Cell> SEARCH_DIRS = List.of(
new Cell(-1,0),
new Cell(0, 1),
new Cell(1, 0),
new Cell(0, -1)
);
public int orangesRotting(int[][] grid) {
if (grid.length == 0) return IMPOSSIBLE_VAL;
Queue<Cell> processingQueue = new ArrayDeque<>();
int freshOranges = 0;
for (int i = 0; i < grid.length; i++) {
for (int j = 0; j < grid[0].length; j++) {
if (grid[i][j] == ROTTON_ORANGE) {
processingQueue.offer(new Cell(i, j));
} else if (grid[i][j] == FRESH_ORANGE) {
freshOranges++;
}
}
}
if (freshOranges == 0) return 0;
int maxR = grid.length, maxC = grid[0].length;
int ticks = -1;
while (!processingQueue.isEmpty()) {
int levelWidth = processingQueue.size();
for (int i = 0; i < levelWidth; i++) {
Cell currentCell = processingQueue.poll();
for (Cell dir : SEARCH_DIRS) {
Cell nextCell = dir.applyOffset(currentCell);
if (nextCell.r() >= 0 && nextCell.r() < maxR
&& nextCell.c() >= 0 && nextCell.c() < maxC
&& grid[nextCell.r()][nextCell.c()] == FRESH_ORANGE) {
// THIS WAS THE BUG: we must mark it rotten immediately
grid[nextCell.r()][nextCell.c()] = ROTTON_ORANGE;
processingQueue.offer(nextCell);
freshOranges--;
}
}
}
ticks++;
}
return freshOranges == 0 ? ticks : IMPOSSIBLE_VAL;
}
}
Trie
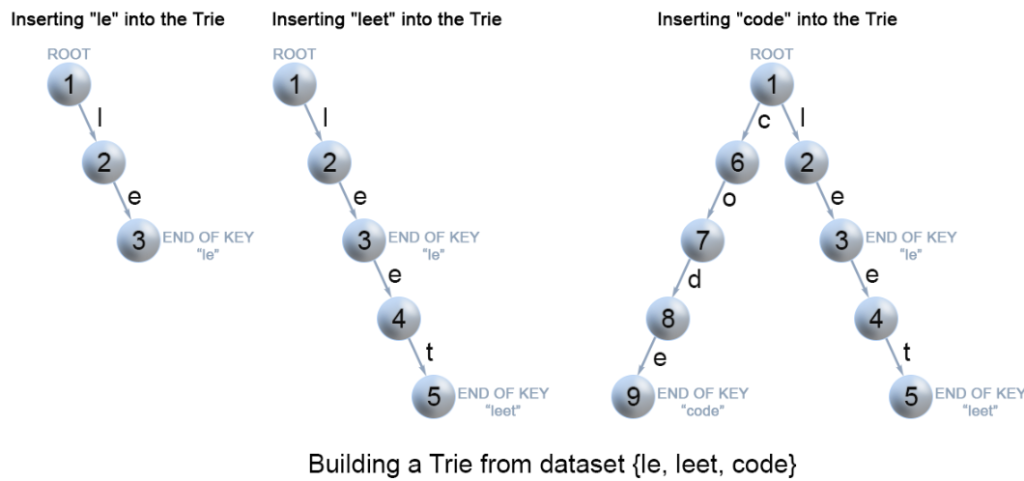
Simple Implementation
- Note: make inner classes static, this way they don’t store a reference (typically 8 bytes) to the outer class in the JVM
- Basically it’s a tree like structure, where each node contains 26 (26 characters) child references to other nodes.

import java.util.Locale;
class Trie {
private static class TrieNode {
private boolean endsWord;
private final TrieNode[] children = new TrieNode[26];
boolean containsKey(char ch) {
return children[ch - 'a'] != null;
}
TrieNode get(char ch) {
return children[ch - 'a'];
}
void put(char ch, TrieNode node) {
children[ch - 'a'] = node;
}
}
private final TrieNode root = new TrieNode();
public void insert(String word) {
TrieNode current = root;
for (char c : word.toLowerCase(Locale.ROOT).toCharArray()) {
if (c < 'a' || c > 'z') continue;
if (!current.containsKey(c)) {
current.put(c, new TrieNode());
}
current = current.get(c);
}
current.endsWord = true;
}
public boolean search(String word) {
TrieNode node = findNode(word);
return node != null && node.endsWord;
}
public boolean startsWith(String prefix) {
return findNode(prefix) != null;
}
private TrieNode findNode(String s) {
TrieNode current = root;
for (char c : s.toLowerCase(Locale.ROOT).toCharArray()) {
if (c < 'a' || c > 'z') return null;
if (!current.containsKey(c)) return null;
current = current.get(c);
}
return current;
}
}
Backtracking
- Usually a good approach when you are asked to find all of something with low bounds
N-Queens: given n*n chess board, how many queens can be placed
Notes:
- Use backtracking approach:
- take each row at a time, iterate over the cols
- if safe to place a queen, place it, then recurse into the next row (carry count of solutions so far)
- if next row would be the end of board, then don’t recurse, increase solution count, return count
- For checking if safe to place a queen, use 3 sets:
- row: don’t need a set for this, we add and remove if safe as we iterate across
- col: maintain a set for any queen place in a col (remove too when backtracking)
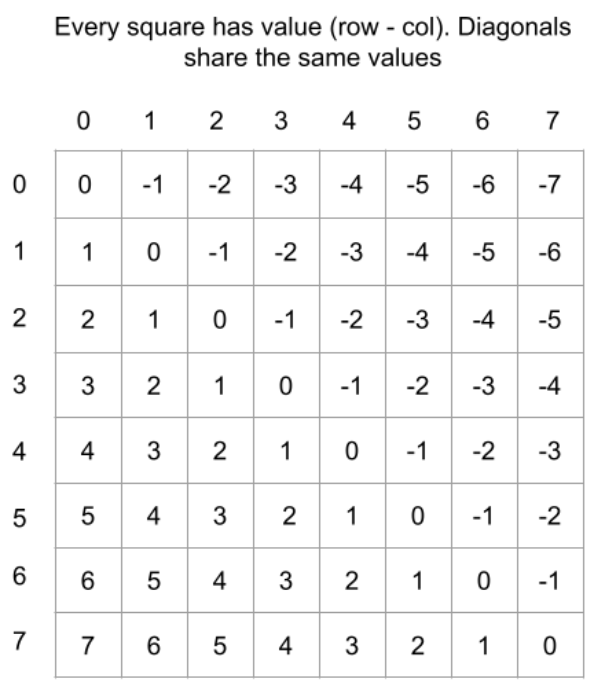
- diagonals:
- trick: diagonals can be identified by a unique number, keep a set of all diagonals that contain a queen (in the going up and going down diagonals)
- going towards top right – notice that row + col uniquely identifies these
- going to bottom right – notice that row – col uniquely identifies these
- Complexity:
- brute force: O(N^N)
- backtrack: O(N!)

class Solution {
private int size;
public int totalNQueens(int n) {
size = n;
return backtrack(0, new HashSet<>(), new HashSet<>(), new HashSet<>());
}
private int backtrack(
int row,
Set<Integer> diagonals,
Set<Integer> antiDiagonals,
Set<Integer> cols
) {
// Base case - N queens have been placed
if (row == size) {
return 1;
}
int solutions = 0;
for (int col = 0; col < size; col++) {
int currDiagonal = row - col;
int currAntiDiagonal = row + col;
// If the queen is not placeable
if (
cols.contains(col) ||
diagonals.contains(currDiagonal) ||
antiDiagonals.contains(currAntiDiagonal)
) {
continue;
}
// "Add" the queen to the board
cols.add(col);
diagonals.add(currDiagonal);
antiDiagonals.add(currAntiDiagonal);
// Move on to the next row with the updated board state
solutions += backtrack(row + 1, diagonals, antiDiagonals, cols);
// "Remove" the queen from the board since we have already
// explored all valid paths using the above function call
cols.remove(col);
diagonals.remove(currDiagonal);
antiDiagonals.remove(currAntiDiagonal);
}
return solutions;
}
}
Template pseudocode for backtracking
def backtrack(candidate):
if find_solution(candidate):
output(candidate)
return
# iterate all possible candidates.
for next_candidate in list_of_candidates:
if is_valid(next_candidate):
# try this partial candidate solution
place(next_candidate)
# given the candidate, explore further.
backtrack(next_candidate)
# backtrack
remove(next_candidate)
Sudoku Solver
- Brute Force Complexity: 9^81
- Backtracking: (9!)^9
- Time complexity is constant here since the board size is fixed and there is no N-parameter to measure. Though let’s discuss the number of operations needed : (9!)9. Let’s consider one row, i.e. not more than 9 cells to fill. There are not more than 9 possibilities for the first number to put, not more than 9×8 for the second one, not more than 9×8×7 for the third one, etc. In total that results in not more than 9! possibilities for just one row, which means no more than (9!)9 operations in total.
Let’s compare:
- Time complexity is constant here since the board size is fixed and there is no N-parameter to measure. Though let’s discuss the number of operations needed : (9!)9. Let’s consider one row, i.e. not more than 9 cells to fill. There are not more than 9 possibilities for the first number to put, not more than 9×8 for the second one, not more than 9×8×7 for the third one, etc. In total that results in not more than 9! possibilities for just one row, which means no more than (9!)9 operations in total.
- Space complexity constant (81)
- Implementation Notes:
- backtracking
- To check if safe to place, maintain 3 sets: column, row, subBox (see how to calculate subbox idx within)
- check if safe, add to board and sets, when removing, remove from board and sets
- need to run over (initialise) the sets before starting
- within the backtracking function, advance across row by row
class Solution {
private static final int BOARD_SIZE = 9;
private static final char EMPTY_VAL = '.';
private List<Set<Character>> columns;
private List<Set<Character>> rows;
// row-major order
private List<Set<Character>> subBoxes;
private char[][] board;
public void solveSudoku(char[][] board) {
if (board.length != BOARD_SIZE || board[0].length != BOARD_SIZE) {
throw new IllegalArgumentException("Invalid board");
}
this.board = board;
int emptyCells = init();
backTrackSolve(0, 0, emptyCells);
}
private boolean backTrackSolve(int row, int col, int emptyCells) {
if (board[row][col] != EMPTY_VAL) {
Pair<Integer, Integer> nextCell = advance(row, col);
return backTrackSolve(nextCell.getKey(), nextCell.getValue(), emptyCells);
}
for (int n = 1; n <= 9; n++) {
char tryChar = (char) ('0' + n);
if (charPlacementIsValid(tryChar, row, col)) {
placeChar(tryChar, row, col);
emptyCells--;
if (emptyCells == 0)
return true;
Pair<Integer, Integer> nextCell = advance(row, col);
if (backTrackSolve(nextCell.getKey(), nextCell.getValue(), emptyCells))
return true;
removeChar(tryChar, row, col);
emptyCells++;
}
}
return false;
}
private Pair<Integer, Integer> advance(int r, int c) {
return new Pair(
c == BOARD_SIZE - 1 ? r + 1 : r,
c == BOARD_SIZE - 1 ? 0 : c + 1);
}
private int init() {
// TODO add validation for each val
columns = new ArrayList<Set<Character>>();
rows = new ArrayList<Set<Character>>();
subBoxes = new ArrayList<Set<Character>>();
int emptyCells = 0;
// initialise lists
for (int i = 0; i < BOARD_SIZE; i++) {
columns.add(new HashSet<Character>());
rows.add(new HashSet<Character>());
subBoxes.add(new HashSet<Character>());
}
for (int r = 0; r < BOARD_SIZE; r++) {
for (int c = 0; c < BOARD_SIZE; c++) {
char val = board[r][c];
if (val == EMPTY_VAL) {
emptyCells++;
continue;
}
columns.get(c).add(val);
rows.get(r).add(val);
subBoxes.get(subBoxForCell(r, c)).add(val);
}
}
return emptyCells;
}
private int subBoxForCell(int r, int c) {
return ((r / 3) * 3) + (c / 3);
}
private boolean charPlacementIsValid(char ch, int r, int c) {
return !(columns.get(c).contains(ch)
|| rows.get(r).contains(ch)
|| subBoxes.get(subBoxForCell(r, c)).contains(ch));
}
private void placeChar(char ch, int r, int c) {
board[r][c] = ch;
columns.get(c).add(ch);
rows.get(r).add(ch);
subBoxes.get(subBoxForCell(r, c)).add(ch);
}
private void removeChar(char ch, int r, int c) {
board[r][c] = EMPTY_VAL;
columns.get(c).remove(ch);
rows.get(r).remove(ch);
subBoxes.get(subBoxForCell(r, c)).remove(ch);
}
}
Combinations
- Given two integers
nandk, return all possible combinations ofknumbers chosen from the range[1, n]. - algo:
- recursively traverse along n, iterate through all remaining numbers adding to a running list, when list size is == k (or consumed k numbers), then add to solution
class Solution {
private int n;
private int k;
List<List<Integer>> ans;
public List<List<Integer>> combine(int n, int k) {
this.ans = new ArrayList<>();
if (k <= 0)
return ans;
this.n = n;
this.k = k;
combineBackTrack(new LinkedList<Integer>(), k, 1);
return ans;
}
private void combineBackTrack(LinkedList<Integer> runningList, int takeCount, int lowerNum) {
for (int i = lowerNum; i <= n; i++) {
runningList.add(i);
if (takeCount - 1 == 0) {
ans.add(new ArrayList(runningList));
} else {
combineBackTrack(runningList, takeCount - 1, i + 1);
}
runningList.removeLast();
}
}
}
Permutations
- Given an array
numsof distinct integers, return all the possible permutations. You can return the answer in any order. - Note: use set (“consumed”) here for efficient tracked of what has been used, discuss with interviwer
class Solution {
private List<List<Integer>> ans;
// could also just search "runningList", but this is slightly more efficient O(1) add, lookup, remove
private Set<Integer> consumed;
int[] nums;
public List<List<Integer>> permute(int[] nums) {
init(nums);
if (nums.length == 0) return ans;
permuteBackTrack(new LinkedList<Integer>(), 0);
return ans;
}
private void permuteBackTrack(LinkedList<Integer> runningList, int idx) {
for (int i = 0; i < nums.length; i++) {
int num = nums[i];
if (consumed.contains(num)) continue;
consumed.add(num);
runningList.add(num);
if (consumed.size() == nums.length) {
ans.add(new ArrayList<Integer>(runningList));
} else {
permuteBackTrack(runningList, idx+1);
}
runningList.removeLast();
consumed.remove(num);
}
}
private void init(int[] nums) {
this.ans = new LinkedList<List<Integer>>();
this.nums = nums;
this.consumed = new HashSet<Integer>();
}
}
Word Search
- Given an
m x ngrid of charactersboardand a stringword, returntrueifwordexists in the grid.
class Solution {
// TODO use record for cell access, better readibility?
private static final Character VISITED_CHAR = '#';
private static record Cell(int r, int c) {
public Cell applyOffset(Cell other) {
return new Cell(this.r() + other.r(), this.c() + other.c());
}
};
private static final List<Cell> SEARCH_DIRS = new ArrayList<>(List.of(
new Cell(0, 1),
new Cell(1, 0),
new Cell(0, -1),
new Cell(-1, 0)
));
private char[][] board;
private String word;
public boolean exist(char[][] board, String word) {
if (board.length == 0
|| word.length() == 0
|| word.length() > (board.length * board[0].length))
return false;
this.board = board;
this.word = word;
for (int r = 0; r < board.length; r++) {
for (int c = 0; c < board[0].length; c++) {
char currentChar = word.charAt(0);
if (currentChar == board[r][c]) {
Cell cell = new Cell(r, c);
board[r][c] = VISITED_CHAR;
if (findWordBacktrack(cell, 0)) return true;
board[r][c] = currentChar;
}
}
}
return false;
}
/**
* invariant (i.e. charAt(0) == board[curCell])
*/
private boolean findWordBacktrack(Cell curCell, int offset) {
// TODO - what if string is size 1
if (offset == word.length() - 1) return true;
int nextOffset = offset + 1;
char nextWordChar = word.charAt(nextOffset);
for (Cell dir : SEARCH_DIRS) {
Cell nextCell = dir.applyOffset(curCell);
if (isCellVisitable(nextCell) && board[nextCell.r()][nextCell.c()] == nextWordChar) {
board[nextCell.r()][nextCell.c()] = VISITED_CHAR;
if (findWordBacktrack(nextCell, nextOffset)) return true;
board[nextCell.r()][nextCell.c()] = nextWordChar;
}
}
return false;
}
private boolean isCellVisitable(Cell cell) {
return cell.r() >= 0 && cell.r() < board.length
&& cell.c() >=0 && cell.c() < board[0].length
&& board[cell.r()][cell.c()] != VISITED_CHAR;
}
}
Divide and Conquer
Convert array to height-balanced binary tree
- sort array first if needed
- then “recursively traverse” the array
- pick middle, set as root
- left is all the nodes to left of middle
- right is all the nodes to right of middle
- when left > right, return null
class Solution {
int[] nums;
public TreeNode helper(int left, int right) {
if (left > right) return null;
// always choose left middle node as a root
int p = (left + right) / 2;
// preorder traversal: node -> left -> right
TreeNode root = new TreeNode(nums[p]);
root.left = helper(left, p - 1);
root.right = helper(p + 1, right);
return root;
}
public TreeNode sortedArrayToBST(int[] nums) {
this.nums = nums;
return helper(0, nums.length - 1);
}
}
Merge Sort
- note: need the 2nd and 3rd while loops in merge() because we advance the points by value not by index
- Here, n is the number of elements in the
numsarray.- Time complexity: O(nlogn)
- We divide the
numsarray into two halves till there is only one element in the array, which will lead to O(logn) steps.
n→n/2→n/4→…→1 (k steps)
n/2(k−1)=1⟹ k≈logn - And after each division, we merge those respective halves which will take O(n) time each.
- Thus, overall it takes O(nlogn) time.
- We divide the
- Space complexity: O(n)
- Time complexity: O(nlogn)
class Solution {
public int[] sortArray(int[] nums) {
if (nums.length == 0 || nums.length == 1) return nums;
mergeSort(nums, 0, nums.length - 1);
return nums;
}
private void mergeSort(int[] nums, int left, int right) {
// root/base case
if (left >= right) return;
int mid = left + (right - left) / 2;
mergeSort(nums, left, mid);
mergeSort(nums, mid+1, right);
merge(nums, left, mid, right);
}
private void merge(int[] nums, int left, int mid, int right) {
int[] temp = new int[right - left + 1];
int lPtr = left;
int rPtr = mid + 1;
int tempPtr = 0;
while (lPtr <= mid && rPtr <= right) {
temp[tempPtr++] = nums[lPtr] <= nums[rPtr] ? nums[lPtr++] : nums[rPtr++];
}
while (lPtr <= mid) {
temp[tempPtr++] = nums[lPtr++];
}
while (rPtr <= right) {
temp[tempPtr++] = nums[rPtr++];
}
for (int i = 0; i < temp.length; i++) {
nums[left+i] = temp[i];
}
}
}
Sort Linked List
- Use merge sort approach
- important points
- Instead of using index based approach, split lists into 2 sublists
- splitAtMid is used to find middle node AND set
midPrev.next = null, which allows us to easily traverse this list later - remember that after while loop in
merge, one of the left or right lists will be exhausted.
- Complexity Analysis
Time Complexity: O(nlogn), where n is the number of nodes in linked list.
The algorithm can be split into 2 phases, Split and Merge.
Let’s assume that n is power of 2. Forn = 16, the split and merge operation in Top Down fashion can be visualized as follows
Split
The recursion tree expands in form of a complete binary tree, splitting the list into two halves recursively. The number of levels in a complete binary tree is given by log2n. For n=16, number of splits = log216=4
Merge
At each level, we merge n nodes which takes O(n) time.
For n=16, we perform merge operation on 16 nodes in each of the 4 levels.
So the time complexity for split and merge operation is O(nlogn)
Space Complexity: O(logn) , where n is the number of nodes in linked list. Since the problem is recursive, we need additional space to store the recursive call stack. The maximum depth of the recursion tree is logn
/**
* Definition for singly-linked list.
* public class ListNode {
* int val;
* ListNode next;
* ListNode() {}
* ListNode(int val) { this.val = val; }
* ListNode(int val, ListNode next) { this.val = val; this.next = next; }
* }
*/
class Solution {
public ListNode sortList(ListNode head) {
if (head == null || head.next == null) return head;
ListNode mid = splitAtMid(head);
ListNode leftList = sortList(head);
ListNode rightList = sortList(mid);
return merge(leftList, rightList);
}
private ListNode merge(ListNode left, ListNode right) {
ListNode sentinelNode = new ListNode(0);
ListNode tail = sentinelNode;
while (left != null && right != null) {
if (left.val <= right.val) {
tail.next = left;
tail = left;
left = left.next;
} else {
tail.next = right;
tail = right;
right = right.next;
}
}
/** IMPORTANT NODE - at this point, either right or left is null (that's where we stopped in while loop),
so we don't have to do this:
if (left != null) {
current.next = left;
while (left.next != null) left = left.next;
current = left;
}
instead, only one of the left or right lists still contains nodes, so we sent the tail that
*/
tail.next = (left != null) ? left : right;
return sentinelNode.next;
}
/**
* Finds the mid node, sets next pointer of node before mid to null
*/
private ListNode splitAtMid(ListNode head) {
ListNode midPrev = null;
while (head != null && head.next != null) {
midPrev = (midPrev == null) ? head : midPrev.next;
head = head.next.next;
}
// IMPORTANT NOTE: spliting here (setting midPrev.next to null) allows us to easily traverse the sublists
// later, by identifying the end of the lists
ListNode mid = midPrev.next;
midPrev.next = null;
return mid;
}
}
Construct Quad Tree
Complexity Analysis
Here N is the side of the matrix.
- Time complexity: O(N^ 2logN).After every level of recursion the original length of matrix get reduced to half, this implies that the size of matrix will reduced down to one after logN iterations. At each of these logN iterations, we will have some number of recursive calls for the current matrix size. For example, initially we have one call for the size of matrix N∗N, then we will have four recursive calls each for matrix of size (N∗N)/4 and so on. The image below represents how at each level the total number of iterations over the matrix cells remains same at N2. Hence, N2 iterations at each of the logN levels makes up the time complexity to be O(N^2 logN).

- Space complexity: O(logN).The space to store the output is generally not part of the space complexity. Hence the only space needed is for the recursion call stack; the maximum number of active stack calls is logN. Therefore, the total space complexity equals O(logN).
class Solution {
public Node construct(int[][] grid) {
int length = grid.length;
if (length == 0) return null;
return constructQuadTree(grid, 0, 0, length);
}
/**
* Computes a quad tree for a grid subsection, where subsection is identified
* by an anchor / starting cell (cell in top left of subgrid) and expands length
* number of rows and cols
*
* @param grid grid from which to construct quadtree
* @param row row of starting cell
* @param col col of start cell
* @param length number of rows and cols in the subgrid
*/
private Node constructQuadTree(int[][] grid, int row, int col, int length) {
// base case, leaf
if (isLeaf(grid, row, col, length)) {
return new Node(grid[row][col] == 1, true);
}
Node node = new Node(false, false);
int subGridLength = length / 2;
node.topLeft = constructQuadTree(grid, row, col, subGridLength);
node.topRight = constructQuadTree(grid, row, col + subGridLength, subGridLength);
node.bottomLeft = constructQuadTree(grid, row + subGridLength, col, subGridLength);
node.bottomRight = constructQuadTree(grid, row + subGridLength, col + subGridLength, subGridLength);
return node;
}
private boolean isLeaf(int[][] grid, int row, int col, int length) {
int val = grid[row][col];
for (int i = 0; i < length; i++) {
for (int j = 0; j < length; j++) {
if (grid[row+i][col+j] != val) return false;
}
}
return true;
}
}
You are given an array of
klinked-listslists, each linked-list is sorted in ascending order.Merge all the linked-lists into one sorted linked-list and return it.
Approach
- Apply merge sort
Complexity Analysis
- Time complexity : O(Nlogk) where k is the number of linked lists.
- We can merge two sorted linked list in O(n) time where n is the total number of nodes in two lists.
- Sum up the merge process and we can get: O(∑i=1log2kN)=O(Nlogk)
- Space complexity : O(1)
- We can merge two sorted linked lists in O(1) space.
class Solution {
public ListNode mergeKLists(ListNode[] lists) {
if (lists.length == 0) return null;
return mergeKListsMs(lists, 0, lists.length - 1);
}
private ListNode mergeKListsMs(ListNode[] lists, int left, int right) {
if (left == right) return lists[left];
int mid = left + (right - left) / 2;
ListNode leftList = mergeKListsMs(lists, left, mid);
ListNode rightList = mergeKListsMs(lists, mid+1, right);
return mergeLists(leftList, rightList);
}
private ListNode mergeLists(ListNode list1, ListNode list2) {
ListNode sentinel = new ListNode(0);
ListNode tail = sentinel;
while (list1 != null && list2 != null) {
if (list1.val < list2.val) {
tail.next = list1;
tail = tail.next;
list1 = list1.next;
} else {
tail.next = list2;
tail = tail.next;
list2 = list2.next;
}
}
//add remaining
if (list1 == null) {
tail.next = list2;
} else {
tail.next = list1;
}
return sentinel.next;
}
}
Binary Search
Binary Search on sorted matrix
- Matrix, rows ascending order, first col in next row has value greater the last val in previous row
- Algo:
- basically treat as a sorted array, perform binary search using location index (location -> matrix: row = location / matrix[0].length; col = location % matrix[0].length – important use cols size in both these places)
- important notes:
- use inclusive indices (see
matrix.length * matrix[0].length - 1) - check for base case:
left > right- note: you check if midIdx has the value, if not => recurse and now remove this checked index (i.e., either check
left -> midIdx -1ormidIdx + 1 -> right, otherwise will be infinite loop
- note: you check if midIdx has the value, if not => recurse and now remove this checked index (i.e., either check
- use inclusive indices (see
class Solution {
public boolean searchMatrix(int[][] matrix, int target) {
if (matrix.length == 0) return false;
return binarySearchMatrix(matrix, 0, matrix.length * matrix[0].length - 1, target);
}
private boolean binarySearchMatrix(int[][] matrix, int left, int right, int target) {
if (left > right) {
return false;
}
int midIdx = left + (right - left) / 2;
Pair<Integer, Integer> midCoOrds = calcCoOrdsFromLocation(matrix, midIdx);
int valAtMid = matrix[midCoOrds.getKey()][midCoOrds.getValue()];
if (valAtMid == target) {
return true;
}
if (target > valAtMid) {
return binarySearchMatrix(matrix, midIdx+1, right, target);
} else {
return binarySearchMatrix(matrix, left, midIdx-1, target);
}
}
private Pair<Integer, Integer> calcCoOrdsFromLocation(int[][] matrix, int location) {
int row = location / matrix[0].length;
int col = location % matrix[0].length;
return new Pair<Integer, Integer>(row, col);
}
}
Binary Search on Rotated Array
- trick can perform modified binary search on rotated array to find offset – compare mid to array[length-1]
- then perform BS as normal, but when accessing the array, use the offset:
array[(bsIdx + offset) % length] - note: even when searching for smallest value, use
left>rightas the base case - note: don’t forget to always use INCLUSIVE indices for BS (i.e.,
0 to length-1)
class Solution {
public int search(int[] nums, int target) {
int length = nums.length;
if (length == 0) return -1;
int rotationOffset = findRotationOffset(nums, 0, length-1);
return offsetBinarySearch(nums, 0, length-1, target, rotationOffset);
}
private int offsetBinarySearch(int[] nums, int left, int right, int target, int offset) {
if (left > right) return -1;
int bsMidIdx = left + (right - left) / 2;
int offsetMidIdx = (bsMidIdx + offset) % nums.length;
int midVal = nums[offsetMidIdx];
if (midVal == target) return offsetMidIdx;
if (target > midVal) {
return offsetBinarySearch(nums, bsMidIdx+1,right, target, offset);
} else {
return offsetBinarySearch(nums, left, bsMidIdx-1,target, offset);
}
}
private int findRotationOffset(int[] nums, int left, int right) {
if (left > right) return left;
int midIdx = left + (right - left) / 2;
int midVal = nums[midIdx];
if (midVal > nums[nums.length-1]) {
return findRotationOffset(nums, midIdx+1, right);
} else {
return findRotationOffset(nums, left, midIdx-1);
}
}
}
Find first and last position of an element in a sorted array
- perform binary search, but what you’re looking for is the edge of the sub array (this is either the edge of the overall array, or the edge of the sub array)
- e.g. Input: nums = [5,7,7,8,8,10], target = 8 Output: [3,4]
class Solution {
public int[] searchRange(int[] nums, int target) {
int[] ans = new int[2];
ans[0] = findSubArrayEdge(nums, 0, nums.length - 1, target, true);
ans[1] = findSubArrayEdge(nums, 0, nums.length - 1, target, false);
return ans;
}
private int findSubArrayEdge(int[] nums, int left, int right, int target, boolean startingEdge) {
if (left > right) return -1;
int midIdx = left + (right - left) / 2;
int midVal = nums[midIdx];
if (midVal == target) {
// target val is at the edge of whole array
if( midIdx == (startingEdge ? 0 : nums.length - 1) ) return midIdx;
// target val is at the edge of sub array
if ( nums[midIdx + (startingEdge ? -1 : 1)] != target ) return midIdx;
return findSubArrayEdge(
nums,
startingEdge ? left : midIdx + 1,
startingEdge ? midIdx - 1 : right,
target,
startingEdge
);
}
if (target > midVal) {
return findSubArrayEdge(nums, midIdx + 1, right, target, startingEdge);
} else {
return findSubArrayEdge(nums, left, midIdx - 1, target, startingEdge);
}
}
}
Find Min Val in sorted array (rotated)
- apply same approach as BS, but use nums[length-1] as the “target” – note – check the comparison op, if
midVal > nums[length-1], then start (min val) of array must be somewhere to the right
class Solution {
public int findMin(int[] nums) {
if (nums.length == 0) return -1;
return nums[bsFindMin(nums, 0, nums.length-1)];
}
private int bsFindMin(int[] nums, int left, int right) {
if (left > right) return left;
int midIdx = left + (right - left) / 2;
int midVal = nums[midIdx];
if (midVal > nums[nums.length-1]) {
return bsFindMin(nums, midIdx+1, right);
} else {
return bsFindMin(nums, left, midIdx-1);
}
}
}
Square Root using Binary Search
notes
- use
longwhen multiplying two ints to store answer!intrange: −2,147,483,648 to 2,147,483,647- Multiplying two large
ints can exceed this range - Java does not throw an error on overflow — it silently wraps
longis 64-bit- Range: about ±9 × 10¹⁸
- Safe for most integer multiplications
class Solution {
public int mySqrt(int x) {
if (x < 2) return x;
long num;
int pivot, left = 2, right = x / 2;
while (left <= right) {
pivot = left + (right - left) / 2;
num = (long) pivot * pivot;
if (num > x) right = pivot - 1;
else if (num < x) left = pivot + 1;
else return pivot;
}
return right;
}
}
Heap
Definition: A complete binary tree that satisfies the heap property
Types:
- Min-heap: parent ≤ children
- Max-heap: parent ≥ children
Array representation:
- Parent:
(i - 1) / 2 - Left child:
2i + 1 - Right child:
2i + 2
Core operations:
- Insert →
O(log n)(heapify up) - Extract min/max →
O(log n)(heapify down) - Peek →
O(1)
Build heap: O(n) using bottom-up heapify
Java: PriorityQueue (min-heap by default)
Common uses: top-K elements, scheduling, Dijkstra, merging sorted lists
Key difference from BST: heap is not sorted, only root is min/max
Implementation
note
- starting at index 1 makes all the indexing easier, don’t
-1when accessing array - parent of an index is always
index/2(integer division)- left child is
index*2 - right child is
index*2+1
- left child is
// Implementing "Min Heap"
public class MinHeap {
// Create a complete binary tree using an array
// Then use the binary tree to construct a Heap
int[] minHeap;
// the number of elements is needed when instantiating an array
// heapSize records the size of the array
int heapSize;
// realSize records the number of elements in the Heap
int realSize = 0;
public MinHeap(int heapSize) {
this.heapSize = heapSize;
minHeap = new int[heapSize + 1];
// To better track the indices of the binary tree,
// we will not use the 0-th element in the array
// You can fill it with any value
minHeap[0] = 0;
}
// Function to add an element
public void add(int element) {
realSize++;
// If the number of elements in the Heap exceeds the preset heapSize
// print "Added too many elements" and return
if (realSize > heapSize) {
System.out.println("Added too many elements!");
realSize--;
return;
}
// Add the element into the array
minHeap[realSize] = element;
// Index of the newly added element
int index = realSize;
// Parent node of the newly added element
// Note if we use an array to represent the complete binary tree
// and store the root node at index 1
// index of the parent node of any node is [index of the node / 2]
// index of the left child node is [index of the node * 2]
// index of the right child node is [index of the node * 2 + 1]
int parent = index / 2;
// If the newly added element is smaller than its parent node,
// its value will be exchanged with that of the parent node
while ( minHeap[index] < minHeap[parent] && index > 1 ) {
int temp = minHeap[index];
minHeap[index] = minHeap[parent];
minHeap[parent] = temp;
index = parent;
parent = index / 2;
}
}
// Get the top element of the Heap
public int peek() {
return minHeap[1];
}
// Delete the top element of the Heap
public int pop() {
// If the number of elements in the current Heap is 0,
// print "Don't have any elements" and return a default value
if (realSize < 1) {
System.out.println("Don't have any element!");
return Integer.MAX_VALUE;
} else {
// When there are still elements in the Heap
// realSize >= 1
int removeElement = minHeap[1];
// Put the last element in the Heap to the top of Heap
minHeap[1] = minHeap[realSize];
realSize--;
int index = 1;
// When the deleted element is not a leaf node
while (index <= realSize / 2) {
// the left child of the deleted element
int left = index * 2;
// the right child of the deleted element
int right = (index * 2) + 1;
// If the deleted element is larger than the left or right child
// its value needs to be exchanged with the smaller value
// of the left and right child
if (minHeap[index] > minHeap[left] || minHeap[index] > minHeap[right]) {
if (minHeap[left] < minHeap[right]) {
int temp = minHeap[left];
minHeap[left] = minHeap[index];
minHeap[index] = temp;
index = left;
} else {
// maxHeap[left] >= maxHeap[right]
int temp = minHeap[right];
minHeap[right] = minHeap[index];
minHeap[index] = temp;
index = right;
}
} else {
break;
}
}
return removeElement;
}
}
// return the number of elements in the Heap
public int size() {
return realSize;
}
public String toString() {
if (realSize == 0) {
return "No element!";
} else {
StringBuilder sb = new StringBuilder();
sb.append('[');
for (int i = 1; i <= realSize; i++) {
sb.append(minHeap[i]);
sb.append(',');
}
sb.deleteCharAt(sb.length() - 1);
sb.append(']');
return sb.toString();
}
}
public static void main(String[] args) {
// Test case
MinHeap minHeap = new MinHeap(3);
minHeap.add(3);
minHeap.add(1);
minHeap.add(2);
// [1,3,2]
System.out.println(minHeap.toString());
// 1
System.out.println(minHeap.peek());
// 1
System.out.println(minHeap.pop());
// [2, 3]
System.out.println(minHeap.toString());
minHeap.add(4);
// Add too many elements
minHeap.add(5);
// [2,3,4]
System.out.println(minHeap.toString());
}
}
Find K-th largest element
- Algo:
- looking for k-th largest element, so add everything to a priority queue
- keep the size of the queue at
kby removing an element whenever size > k - this will result in the queue containing the top k largest elements, prioritised in ascending order
- then peeking will reveal the k-th largest element
- complexity:
- space: O(k) (delete everything after kth element
- complexity
- O(n + n * log k)
Note: max heap / min heap using priority queues
// Construct an instance of Max Heap PriorityQueue<Integer> maxHeap = new PriorityQueue<>(Collections.reverseOrder()); PriorityQueue<Integer> minHeap = new PriorityQueue<>();
class Solution {
public int findKthLargest(int[] nums, int k) {
PriorityQueue<Integer> queue = new PriorityQueue<Integer>();
for (int num : nums) {
queue.offer(num);
if (queue.size() > k) queue.remove();
}
return queue.peek();
}
}
Find K-Pairs with Smallest sums
You are given two integer arrays
nums1andnums2sorted in non-decreasing order and an integerk.Define a pair
(u, v)which consists of one element from the first array and one element from the second array.Return the
kpairs(u1, v1), (u2, v2), ..., (uk, vk)with the smallest sums.Example 1:
Input: nums1 = [1,7,11], nums2 = [2,4,6], k = 3 Output: [[1,2],[1,4],[1,6]] Explanation: The first 3 pairs are returned from the sequence: [1,2],[1,4],[1,6],[7,2],[7,4],[11,2],[7,6],[11,4],[11,6]
- brute force method:
- add all pairs to priority queue, sorted by sum, min heap
class Solution {
public List<List<Integer>> kSmallestPairs(int[] nums1, int[] nums2, int k) {
PriorityQueue<Pair<Integer, Integer>> q = new PriorityQueue<Pair<Integer, Integer>>(
(a, b) -> {
return Integer.compare(
a.getKey() + a.getValue(),
b.getKey() + b.getValue());
});
for (int num1 : nums1) {
for (int num2 : nums2) {
q.offer(new Pair<Integer, Integer>(num1, num2));
}
}
List<List<Integer>> ans = new ArrayList<List<Integer>>();
for (int i = 0; i < k; i++) {
Pair<Integer, Integer> element = q.poll();
ans.add(new ArrayList<Integer>(List.of(element.getKey(), element.getValue())));
}
return ans;
}
}
- But arrays are sorted, so let’s take advantage
- BEST FIRST SEARCH USING MIN HEAP
- basically, perform BFS, but use a min heap, which will prioritise the next smallest. It also makes sure to eventually visit ALL combinations (up to K or max size)
- NOTE:
- BFS INFECTION – always mark first node as visited, always mark as visited as same time as adding to queue
class Solution {
public List<List<Integer>> kSmallestPairs(int[] nums1, int[] nums2, int k) {
int m = nums1.length;
int n = nums2.length;
List<List<Integer>> ans = new ArrayList<>();
Set<Pair<Integer, Integer>> visited = new HashSet<>();
PriorityQueue<int[]> minHeap = new PriorityQueue<>((a, b)->(a[0] - b[0]));
minHeap.offer(new int[]{nums1[0] + nums2[0], 0, 0});
visited.add(new Pair<Integer, Integer>(0, 0));
while (k-- > 0 && !minHeap.isEmpty()) {
int[] top = minHeap.poll();
int i = top[1];
int j = top[2];
ans.add(List.of(nums1[i], nums2[j]));
if (i + 1 < m && !visited.contains(new Pair<Integer, Integer>(i + 1, j))) {
minHeap.offer(new int[]{nums1[i + 1] + nums2[j], i + 1, j});
visited.add(new Pair<Integer, Integer>(i + 1, j));
}
if (j + 1 < n && !visited.contains(new Pair<Integer, Integer>(i, j + 1))) {
minHeap.offer(new int[]{nums1[i] + nums2[j + 1], i, j + 1});
visited.add(new Pair<Integer, Integer>(i, j + 1));
}
}
return ans;
}
}
Maximise Profits
Suppose LeetCode will start its IPO soon. In order to sell a good price of its shares to Venture Capital, LeetCode would like to work on some projects to increase its capital before the IPO. Since it has limited resources, it can only finish at most
kdistinct projects before the IPO. Help LeetCode design the best way to maximize its total capital after finishing at mostkdistinct projects.You are given
nprojects where theithproject has a pure profitprofits[i]and a minimum capital ofcapital[i]is needed to start it.Initially, you have
wcapital. When you finish a project, you will obtain its pure profit and the profit will be added to your total capital.Pick a list of at most
kdistinct projects from given projects to maximize your final capital, and return the final maximized capital.The answer is guaranteed to fit in a 32-bit signed integer.
Example 1:
Input: k = 2, w = 0, profits = [1,2,3], capital = [0,1,1]
Output: 4
Explanation: Since your initial capital is 0, you can only start the project indexed 0.
After finishing it you will obtain profit 1 and your capital becomes 1.
With capital 1, you can either start the project indexed 1 or the project indexed 2.
Since you can choose at most 2 projects, you need to finish the project indexed 2 to get the maximum capital.
Therefore, output the final maximized capital, which is 0 + 1 + 3 = 4.
Algo
- Break problem down:
- if k == 1, we would iterate through all possible projects (i.e., w >= capital), then we would return that profit
- when k > 1, we must try to take the most profitable projects from the remaining possible projects
- Approach
- build helper class for projects
- sort by increasing capital
- iterate through 0 .. k
- iterate through this list through all possible projects for current w (which could have increased), adding to a heap (that sorts by decreasing profits)
- poll from queue and add to ans – if queue empty, return ans
complexity:
Let n be the number of projects.
- Time complexity: O(nlogn). Sorting the projects by increasing
capitaltakes O(nlogn) time. Also, we perform O(n) operations with the priority queue, each in O(logn). - Space complexity: O(n). The sorted array of projects and the priority queue take linear space.
class Solution {
private class Project {
public int capitalRequired;
public int earnings;
public Project(int capitalRequired, int earnings) {
this.capitalRequired = capitalRequired;
this.earnings = earnings;
}
public int getCapitalRequired() {
return this.capitalRequired;
}
public int getEarnings() {
return this.earnings;
}
}
public int findMaximizedCapital(int k, int w, int[] profits, int[] capital) {
if (profits.length != capital.length) throw new IllegalArgumentException("Invalid projects");
if (k == 0 || profits.length == 0) return w;
List<Project> projects = new ArrayList<Project>();
for (int i = 0; i < profits.length; i++) {
projects.add(new Project(capital[i], profits[i]));
}
projects.sort(Comparator.comparingInt(Project::getCapitalRequired));
PriorityQueue<Project> projectQueue = new PriorityQueue<Project>(Comparator.comparingInt(Project::getEarnings).reversed());
int pIdx = 0;
for (int i = 0; i < k; i++) {
while (pIdx < projects.size() && projects.get(pIdx).getCapitalRequired() <= w) {
projectQueue.offer(projects.get(pIdx));
pIdx++;
}
if (projectQueue.isEmpty()) break;
Project nextProject = projectQueue.poll();
w += nextProject.getEarnings();
}
return w;
}
}
Find median from data stream
The median is the middle value in an ordered integer list. If the size of the list is even, there is no middle value, and the median is the mean of the two middle values.
- For example, for
arr = [2,3,4], the median is3.- For example, for
arr = [2,3], the median is(2 + 3) / 2 = 2.5.Implement the MedianFinder class:
MedianFinder()initializes theMedianFinderobject.void addNum(int num)adds the integernumfrom the data stream to the data structure.double findMedian()returns the median of all elements so far. Answers within10-5of the actual answer will be accepted.
Approach:
- We use a maxHeap called
lowto store all the low numbers (that is if we take all numbers up to this point, sort them, and store half of them), callingpeek()will give us the middle if number count is odd, if the left middle in even count. Same forhigh, but this is a minHeap
Complexity:
- Time complexity: O(5⋅logn)+O(1)≈O(logn).
- At worst, there are three heap insertions and two heap deletions from the top. Each of these takes about O(logn) time.
- Finding the median takes constant O(1) time since the tops of heaps are directly accessible.
- Space complexity: O(n) linear space to hold input in containers.
class MedianFinder {
PriorityQueue<Integer> high = new PriorityQueue<Integer>();
PriorityQueue<Integer> low = new PriorityQueue<Integer>(Collections.reverseOrder());
public MedianFinder() {
}
public void addNum(int num) {
low.offer(num);
// balancing step
high.offer(low.poll());
// maintain size property, ensure distributed across heaps
if (low.size() < high.size()) {
low.offer(high.poll());
}
}
public double findMedian() {
return low.size() > high.size() ? low.peek() : ((double) low.peek() + high.peek()) / 2.0;
}
}
You are given an array of
klinked-listslists, each linked-list is sorted in ascending order.Merge all the linked-lists into one sorted linked-list and return it.
Approach:
- use a heap / priority queue to traverse all the lists in ascending order
- add heads of each list to queue
- keep popping from queue and adding to list, adding node.next back to queue (if not null), and add
Complexity:
- Time complexity : O(Nlogk) where k is the number of linked lists.
- The comparison cost will be reduced to O(logk) for every pop and insertion to priority queue. But finding the node with the smallest value just costs O(1) time.
- There are N nodes in the final linked list.
- Space complexity :
- O(n) Creating a new linked list costs O(n) space.
- O(k) The code above present applies in-place method which cost O(1) space. And the priority queue (often implemented with heaps) costs O(k) space (it’s far less than N in most situations).
class Solution {
public ListNode mergeKLists(ListNode[] lists) {
if (lists.length == 0) return null;
ListNode sentinel = new ListNode(0);
ListNode tail = sentinel;
PriorityQueue<ListNode> q = new PriorityQueue<ListNode>(Comparator.comparingInt(n -> n.val));
//prime the queue with the heads of each list
for (ListNode node : lists) {
if (node != null) {
q.offer(node);
}
}
while (!q.isEmpty()) {
ListNode node = q.poll();
if (node.next != null) {
q.offer(node.next);
}
tail.next = node;
tail = node;
}
return sentinel.next;
}
}
Targeted Questions
Given a string
srepresenting a valid expression, implement a basic calculator to evaluate it, and return the result of the evaluation.Note: You are not allowed to use any built-in function which evaluates strings as mathematical expressions, such as
eval().Example 1:
Input: s = "1 + 1" Output: 2Example 2:
Input: s = " 2-1 + 2 " Output: 3Example 3:
Input: s = "(1+(4+5+2)-3)+(6+8)" Output: 23
- Some important things to note here:
- + is commutative and associative, but – is neither
- also if using a stack approach, this changes order of evaluation from left-right to right-left, so traverse the expression backwards
- Approach:
- stack for ops, operands, brackets
- iterate backwards
- careful building nums – see code below, build powers of 10
- think of it as
- pushing to stack in reverse order
- we don’t evaluate anything outside parens or “root level” until end, we DO evaluate anything within parens whenever we encounter an opening paren, i.e. in this example
1 + (2+3) + 4- we push (from bottom) 4, +, ), 3, +, 2, then when we see ( we evaluate until ), so stack will now be (from bottom) 4, +, 5
- gotchas
- don’t forget to push 0 to stack during evaluation if top of stack is – (example:
1-(-2)) - don’t forget to finish building number after main for loop
- don’t forget to push 0 to stack during evaluation if top of stack is – (example:
class Solution {
private static final char SPACE = ' ';
private static final char PLUS = '+';
private static final char MINUS = '-';
private static final Set<Character> OPS = Set.of(PLUS, MINUS);
private static final char CLOSING_PAREN = ')';
private static final char OPENING_PAREN = '(';
private static enum TokenType {
OP,
NUM,
OPEN_PAREN,
CLOSE_PAREN;
public static TokenType fromChar(char c) {
if (c == '(') return OPEN_PAREN;
else if (c == ')') return CLOSE_PAREN;
else if (OPS.contains(c)) return OP;
else return NUM;
}
}
private static class Token {
// TODO getters / setters
public int val;
public TokenType type;
public char rawChar;
public Token(int val) {
this.val = val;
this.type = TokenType.NUM;
this.rawChar = SPACE;
}
public Token(char rawChar, TokenType type) {
this.rawChar = rawChar;
this.type = type;
this.val = Integer.MIN_VALUE;
}
}
public int calculate(String s) {
if (s.length() == 0) throw new IllegalArgumentException("Invalid expression " + s);
Stack<Token> tokenStack = new Stack<Token>();
int numberTens = 0;
int numberVal = 0;
for (int i = s.length() - 1; i >= 0; i--) {
char currentChar = s.charAt(i);
if (currentChar == SPACE) continue;
if (Character.isDigit(currentChar)) {
// 123: 3 * 10^0, 2 * 10^1, 1 * 10^2
numberVal += Math.pow(10, numberTens++) * (currentChar - '0');
} else {
if (numberTens > 0) {
// finished parsing number, compute val
tokenStack.push(new Token(numberVal));
numberTens = 0;
numberVal = 0;
}
// we use s[i] != digit to identify end of number, need to continue processing
// if finished sub expression, i.e. '(', evaluate sub expression
if (currentChar == OPENING_PAREN) {
int subExprResult = evaluateStack(tokenStack);
tokenStack.pop(); //remove closing paren
tokenStack.push(new Token(subExprResult));
} else {
// push everything else
tokenStack.push(new Token(currentChar, TokenType.fromChar(currentChar)));
}
}
}
if (numberTens > 0) {
// finished parsing number, compute val
tokenStack.push(new Token(numberVal));
}
return evaluateStack(tokenStack);
}
private int evaluateStack(Stack<Token> tokenStack) {
if (tokenStack.isEmpty() || tokenStack.peek().type != TokenType.NUM) {
tokenStack.push(new Token(0));
}
int result = tokenStack.pop().val;
while (!tokenStack.isEmpty() && tokenStack.peek().rawChar != CLOSING_PAREN) {
char op = tokenStack.pop().rawChar; //TODO validation
if (op == PLUS) {
result += tokenStack.pop().val;
} else {
result -= tokenStack.pop().val;
}
}
return result;
}
}
Given a string
swhich represents an expression, evaluate this expression and return its value.The integer division should truncate toward zero.
You may assume that the given expression is always valid. All intermediate results will be in the range of
[-231, 231 - 1].Note: You are not allowed to use any built-in function which evaluates strings as mathematical expressions, such as
eval().Example 1:
Input: s = "3+2*2" Output: 7Example 2:
Input: s = " 3/2 " Output: 1Example 3:
Input: s = " 3+5 / 2 " Output: 5
- Approach
- use a stack, but all values in stack will be added (
+) together - when encounter a
-, add the succeeding number to stack as the negative (i.e. “3-4”, stack (from bottom): [3,-4] - store
previousOperation, start with+(think of it as starting with0 + ... - only attempt to evaluate operations AFTER reading a new operation or end of expression
- if + or – simply push value to stack (make sure to make num – if previousOp was
-) - if
*or/, evaluate immediately by popping left operand from stack, then push result to stack
- if + or – simply push value to stack (make sure to make num – if previousOp was
- use a stack, but all values in stack will be added (
Gotchas:
- Don’t skip spaces early, need to enter second main
ifto process last number in expression, see!Character.isDigit(c) && !Character.isWhitespace(c) || i == expressionLen - 1
class Solution {
private static final char SPACE = ' ';
public int calculate(String s) {
int expressionLen = s.length();
if (expressionLen == 0)
throw new IllegalArgumentException("Invalid input: " + s);
Stack<Integer> stack = new Stack<Integer>();
int runningNumber = 0;
// start with +, if leading - in expression, e.g. -1 + 2, will add zero first, i.e. stack is (from bottom) 0,-1,2
char previousOperation = '+';
for (int i = 0; i < s.length(); i++) {
char c = s.charAt(i);
if (Character.isDigit(c)) {
runningNumber = (runningNumber * 10) + c - '0';
}
// not digit (so, operation) OR last char in expression
// important, don't skip space before this, need to enter this if on last char, even if whitespace
// i.e., ends with space
if (!Character.isDigit(c) && !Character.isWhitespace(c) || i == expressionLen - 1) {
if (previousOperation == '*') {
stack.push(stack.pop() * runningNumber);
} else if (previousOperation == '/') {
stack.push(stack.pop() / runningNumber);
} else if (previousOperation == '-') {
stack.push(-runningNumber);
} else if (previousOperation == '+') {
stack.push(runningNumber);
}
previousOperation = c;
runningNumber = 0;
}
}
int result = 0;
while (!stack.isEmpty()) {
result += stack.pop();
}
return result;
}
}
A tidier solution, note:
- appending
@to expression to help with recognising the end of expression - using helper function
evaluate()
class Solution {
private int evaluate(char operator, int x, int y) {
if (operator == '+') {
return x;
} else if (operator == '-') {
return -x;
} else if (operator == '*') {
return x * y;
}
return x / y;
}
public int calculate(String s) {
Stack<Integer> stack = new Stack<>();
int curr = 0;
char previousOperator = '+';
s += "@";
for (char c: s.toCharArray()) {
if (c == ' ') {
continue;
}
if (Character.isDigit(c)) {
curr = curr * 10 + Character.getNumericValue(c);
} else {
if (previousOperator == '*' || previousOperator == '/') {
stack.push(evaluate(previousOperator, stack.pop(), curr));
} else {
stack.push(evaluate(previousOperator, curr, 0));
}
curr = 0;
previousOperator = c;
}
}
int ans = 0;
for (int num: stack) {
ans += num;
}
return ans;
}
}
Implement a basic calculator to evaluate a simple expression string.
The expression string contains only non-negative integers,
'+','-','*','/'operators, and open'('and closing parentheses')'. The integer division should truncate toward zero.You may assume that the given expression is always valid. All intermediate results will be in the range of
[-231, 231 - 1].Note: You are not allowed to use any built-in function which evaluates strings as mathematical expressions, such as
eval().Example 1:
Input: s = "1+1" Output: 2Example 2:
Input: s = "6-4/2" Output: 4Example 3:
Input: s = "2*(5+5*2)/3+(6/2+8)"
Output: 21
Approach:
- Same as basic calc 2, but when you encounter a
(, tackle the subexpression recursively. - Treat result from recursive call as the new runningNum (right operand)
class Solution {
private static final char SPACE = ' ';
private static final char PLUS = '+';
private static final char MINUS = '-';
private static final char DIVIDE = '/';
private static final char MULT = '*';
private static final char OPEN_PAREN = '(';
private static final char CLOSE_PAREN = ')';
private static final char STOP_TOKEN = ';';
private int offset; // consider using array instead (copy of reference to object, global visibility)
private String expression;
public int calculate(String s) {
if (s.length() == 0) throw new IllegalArgumentException("Invalid expression");
expression = s + STOP_TOKEN;
offset = 0;
return performCalculate();
}
public int performCalculate() {
Stack<Integer> stack = new Stack<Integer>();
int runningNum = 0;
char prevOperator = PLUS;
while (offset < expression.length()) {
char currentChar = expression.charAt(offset);
if (currentChar == SPACE) continue;
if (Character.isDigit(currentChar)) {
runningNum = runningNum * 10 + currentChar - '0';
}
if (currentChar == OPEN_PAREN) {
offset++;
runningNum = performCalculate();
}
if (!Character.isDigit(currentChar)) {
if (prevOperator == PLUS) {
stack.push(runningNum);
} else if (prevOperator == MINUS) {
stack.push(-runningNum);
} else if (prevOperator == MULT) {
stack.push(stack.pop() * runningNum);
} else if (prevOperator == DIVIDE) {
stack.push(stack.pop() / runningNum);
}
if (currentChar == CLOSE_PAREN) {
break;
}
runningNum = 0;
prevOperator = currentChar;
}
offset++;
}
int result = 0;
while(!stack.isEmpty()) {
result += stack.pop();
}
return result;
}
}
Implement a SnapshotArray that supports the following interface:
SnapshotArray(int length)initializes an array-like data structure with the given length. Initially, each element equals 0.void set(index, val)sets the element at the givenindexto be equal toval.int snap()takes a snapshot of the array and returns thesnap_id: the total number of times we calledsnap()minus1.int get(index, snap_id)returns the value at the givenindex, at the time we took the snapshot with the givensnap_idExample 1:
Input: ["SnapshotArray","set","snap","set","get"] [[3],[0,5],[],[0,6],[0,0]] Output: [null,null,0,null,5] Explanation: SnapshotArray snapshotArr = new SnapshotArray(3); // set the length to be 3 snapshotArr.set(0,5); // Set array[0] = 5 snapshotArr.snap(); // Take a snapshot, return snap_id = 0 snapshotArr.set(0,6); snapshotArr.get(0,0); // Get the value of array[0] with snap_id = 0, return 5
Approach:
- Create an array of objects that can track all snapshotted values at that index
- Use TreeMap as the object, and the key is snapshot ID to value
- initialise for snapshot == 0 and value == 0
Complexity Analysis
Let n be the maximum number of calls and k = length.
- Time complexity: O(nlogn+k)
- We initialize
historyRecordswith sizek. - In the worst-case scenario, the number of calls to
get,set, andsnapare all O(n). - For each call to
get(index, snap_id), we will perform a binary search over the list of records ofnums[index]. Since a list contains at most O(n) records, a binary search takes O(logn) time on average. Thus it requires O(nlogn) time. - Each call to
snaptakes O(1) time. - Each call to
set(index, snap_id)appends a pair to the historical record ofnums[index], which takes O(1) time, or O(logn) in Java as we are using TreeMap.
- We initialize
- Space complexity: O(n+k)
- We initialize
historyRecordswith sizek. - We add one pair
(snap_id, val)for each call toset, thus there are at most n pairs saved inhistory_record.
- We initialize
class SnapshotArray {
/**
List of TreeMaps
List:
each index contains value at that index
TreeMap:
each map contains all the historical snapshotted avlues
*/
private List<TreeMap<Integer, Integer>> historicalValueArray;
private Integer snapshot;
private int arraySize;
public SnapshotArray(int length) {
historicalValueArray = new ArrayList<TreeMap<Integer, Integer>>();
// initialise array to 0s (i.e., all 0 and snapshot = 0)
for (int i = 0; i < length; i++) {
TreeMap<Integer, Integer> map = new TreeMap<Integer, Integer>();
map.put(0,0);
historicalValueArray.add(map);
}
snapshot = 0;
arraySize = length;
}
public void set(int index, int val) {
if (index < 0 || index >= arraySize) return;
historicalValueArray.get(index).put(snapshot, val);
}
public int snap() {
return snapshot++;
}
public int get(int index, int snap_id) {
if (index < 0 || index >= arraySize) throw new RuntimeException("oob");
if (snap_id < 0 || snap_id > snapshot) throw new RuntimeException("oob");
TreeMap<Integer, Integer> map = historicalValueArray.get(index);
Map.Entry<Integer, Integer> entry = map.floorEntry(snap_id);
return entry.getValue();
}
}
Spammer Detection
Simple find spammer, anyone who sends more than T messages
- Always check for null event!
- discuss with interview if T <= 0 do we accept ANY messages
- in this case do
Math.max(T, 1)
- in this case do
public static Set<String> findSpammers(List<Event> events, int T) {
Set<String> spammers = new HashSet<String>();
if (events == null || events.isEmpty()) return spammers; // TODO emit metrics/logs
// tracks sent message count per sender
Map<String, Integer> senderMessageCount = new HashMap<String,Integer>();
for (Event event : events) {
if (event == null) continue;
String sender = event.sender;
// don't necessarily need this one
String recipient = event.recipient;
// defend invalid events
if (sender == null || sender.isEmpty()
|| recipient == null || recipient.isEmpty()) {
// carefull with logging here in production systems, instead increment metric
System.out.println("Invalid event: " + event.toString());
continue;
}
// track counts
senderMessageCount.merge(sender, 1, Integer::sum);
// detect spammer
if (senderMessageCount.get(sender) >= Math.max(T, 1)) {
spammers.add(sender);
}
}
return spammers;
}
Unique Recipients
Time: O(n)
Space: O(#unique (sender,recipient))
public static Set<String> findSpammers(List<Event> events, int T) {
Set<String> spammers = new HashSet<String>();
// validation
if (events == null || events.isEmpty()) return spammers;
// map of all unique recipients for sender
Map<String, Set<String>> sendersUniqueRecipients = new HashMap<String, Set<String>>();
for (Event event : events) {
// validations
if (event == null) continue;
String sender = event.sender;
String recipient = event.recipient;
// validity: must have non-null and non-empty sender AND recipient
if (sender == null || sender.isEmpty()
|| recipient == null || recipient.isEmpty()) {
continue; // count and emit metric at end for vis
}
Set<String> recipientSet = sendersUniqueRecipients.computeIfAbsent(sender, s -> new HashSet<>(Set.of()));
recipientSet.add(recipient);
if (recipientSet.size() >= Math.max(T, 1)) {
spammers.add(sender);
}
}
return spammers;
}
TOP K spammers
O(n) for initial building map
O(r log r) for sorting and finding top k (more specifically: O(r log r * (1+expectedTieCost)))
public static List<String> topKSpammers(List<Event> events, int T, int K) {
List<String> spammers = new ArrayList<String>();
// validation
if (
events == null || events.isEmpty() // invalid events
|| K <= 0 // invalid or shortcut for K
) return spammers;
int threshold = Math.max(T, 1);
// collects unique recipients for each sender
Map<String, Set<String>> senderData = new HashMap<>();
// collate sender data, unique recipients
for (Event event : events) {
if (event == null) continue;
String sender = event.sender;
String recipient = event.recipient;
if (sender == null || sender.isEmpty()
|| recipient == null || recipient.isEmpty()) continue; // TODO: count, emit metric
Set<String> recipientSet = senderData.computeIfAbsent(sender, s -> new HashSet<>());
recipientSet.add(recipient);
}
// sort by recipient set size DESC, then sender name ASC
senderData.entrySet().stream()
// O(1) iterate lazily, unless forced materialization later (i.e., sorting)
// space - holds remaining after filtering, O(R)
.filter(e -> e.getValue().size() >= threshold)
// of remaining entries O(r log r)
// note if ties, then comparison is O(L) (size of sender names) so O(r log r * (1+expectedTieCost))
.sorted((a,b) -> {
int aRecSize = a.getValue().size();
int bRecSize = b.getValue().size();
if (aRecSize == bRecSize) return a.getKey().compareTo(b.getKey());
else return Integer.compare(bRecSize, aRecSize);
})
.limit(K)
.forEach(e -> spammers.add(e.getKey()));
return spammers;
}
more efficient with heap
| Version | Ranking approach | Time complexity (overall) | Extra space (beyond senderData map/sets) | Why it differs |
|---|
| Sort-all | Filter spammers → sort all qualifying senders → take first K | Build sets: O(n); Ranking: O(R log R); Total: O(n + R log R) (worst-case O(n + S log S)) | O(R) (buffer to sort filtered entries) + output O(min(K,R)) | Sorting needs all R items materialized and ordered before it can apply limit(K); limit doesn’t save work because it happens after sorted. |
| Heap top-K | Filter spammers → maintain min-heap size K (evict worst) → final sort of ≤K | Build sets: O(n); Ranking: O(R log K); Final sort: O(K log K); Total: O(n + R log K + K log K) | O(K) heap + O(K) for final list + output O(K) | Heap avoids sorting all spammers: it only keeps the best K so each qualifying sender costs log K instead of participating in a full log R sort; memory scales with K, not R. |
public static record SenderData(String name, int numUniqueRecipients) implements Comparable<SenderData> {
@Override
public int compareTo(SenderData other) {
int numCompare = Integer.compare(numUniqueRecipients, other.numUniqueRecipients);
if (numCompare != 0) return numCompare;
return other.name.compareTo(name);
}
}
/**
* TODO: Implement me.
*
* Return a list of senderIds for the top K spammers under the ordering rules.
*/
public static List<String> topKSpammers(List<Event> events, int T, int K) {
List<String> spammers = new ArrayList<String>();
// validation
if (
events == null || events.isEmpty() // invalid events
|| K <= 0 // invalid or shortcut for K
) return spammers;
int threshold = Math.max(T, 1);
// collects unique recipients for each sender
Map<String, Set<String>> senderData = new HashMap<>();
// collate sender data, unique recipients
for (Event event : events) {
if (event == null) continue;
String sender = event.sender;
String recipient = event.recipient;
if (sender == null || sender.isEmpty()
|| recipient == null || recipient.isEmpty()) continue; // TODO: count, emit metric
Set<String> recipientSet = senderData.computeIfAbsent(sender, s -> new HashSet<>());
recipientSet.add(recipient);
}
// min heap based on uniqueRecipients count, then name
PriorityQueue<SenderData> senderDataHeap = new PriorityQueue<>();
// collect largest sender data who qualify as spammers in heap of size K
for (Map.Entry<String, Set<String>> data : senderData.entrySet()) {
String name = data.getKey();
int uniqueRecipients = data.getValue().size();
if (uniqueRecipients < threshold) continue;
SenderData sd = new SenderData(name, uniqueRecipients);
if (senderDataHeap.size() < K) {
senderDataHeap.add(sd);
} else {
if (sd.compareTo(senderDataHeap.peek()) > 0) {
senderDataHeap.poll();
senderDataHeap.offer(sd);
}
}
}
List<SenderData> spammerSenderDataList = new ArrayList<>(senderDataHeap);
spammerSenderDataList.sort((a,b) -> {
int cmp = Integer.compare(b.numUniqueRecipients(), a.numUniqueRecipients());
if (cmp != 0) return cmp;
return a.name().compareTo(b.name());
});
for (SenderData sd : spammerSenderDataList) spammers.add(sd.name());
return spammers;
}
Spammers identified if they sent but dont receive T message to/from distinct people
Note:
- records are immutable, but underlying mutable objects can be mutated, just be careful, use class if in doubt
Definitions (so we’re precise)
Let:
- n = total input events (including duplicates)
- nᵥ = number of valid events after filtering (null/empty/self)
(nᵥ ≤ n) - S = number of unique entities (distinct IDs appearing as sender or recipient)
- E = number of unique directed edges
(sender, recipient)among valid events
(i.e., distinct pairs; duplicates collapse in sets)
For a given entity v:
- out(v) =
|sentTo(v)|= number of unique recipients v messaged - in(v) =
|receivedFrom(v)|= number of unique senders who messaged v
Then:
Σ out(v) = EΣ in(v) = E
(because every unique directed edge contributes once to someone’s out-set and once to someone’s in-set)
Build phase complexity (the for (Event event : events) loop)
Time
Each valid event does:
computeIfAbsent(sender)average O(1)sentTo.add(recipient)average O(1) amortizedcomputeIfAbsent(recipient)average O(1)receivedFrom.add(sender)average O(1) amortized
So:
- Expected time: O(nᵥ)
- Worst-case time: can degrade toward O(nᵥ²) with adversarial hashing, but interviews assume average-case hashing unless stated otherwise.
Space
You store:
senderDataMap: O(S) entries- All
sentToedges: total sizeΣ out(v) = E - All
receivedFromedges: total sizeΣ in(v) = E
So total set-element storage is about 2E references (plus hash table overhead).
- Space: O(S + E) (big-O), with a constant factor ~2 for storing edges twice.
Key point: This is already the dominant memory cost. The later
removeAlltemporary sets are extra.
Evaluation phase complexity (the second loop over the map)
You do, for each entity v:
Set<String> distinctUnreplied = new HashSet<>(sentTo); distinctUnreplied.removeAll(receivedFrom); return distinctUnreplied.size();
Let’s analyze that carefully.
Time per entity v
new HashSet<>(sentTo)takes O(out(v)) to copy.removeAll(receivedFrom):- For
HashSet.removeAll(Collection c), the implementation typically iterates overcand doesremoveon the target set. - So expected cost is O(|c|) removals, each O(1) average.
- Here
c = receivedFrom(v)so cost ~ O(in(v)).
- For
So per entity:
- Expected time: O(out(v) + in(v))
Total evaluation time across all entities
Sum over all v:
Σ (out(v) + in(v)) = Σ out(v) + Σ in(v) = E + E = 2E
So:
- Expected evaluation time: O(E)
And since E ≤ nᵥ, you can also say evaluation is O(nᵥ) in the worst case where most events are unique.
Extra space during evaluation
This is the important hidden cost:
- For each entity, you allocate
distinctUnrepliedof size out(v). - Peak extra memory at any moment is O(max_v out(v)) because you allocate it per entity and discard before the next (assuming GC keeps up).
- But total allocated over the run is
Σ out(v) = Eelements worth of churn. That’s a performance concern even if peak memory is bounded.
So:
- Peak extra space: O(max out(v))
- Allocation churn: Θ(E) elements allocated across the whole evaluation
In interviews, I’d call this out as “extra allocation overhead”.
End-to-end complexity (your current approach)
Expected time
- Build: O(nᵥ)
- Evaluate: O(E)
So overall:
- O(nᵥ + E)
Since E ≤ nᵥ always (unique edges can’t exceed events), you can simplify:
- O(nᵥ) expected time (or O(n) if you don’t distinguish valid)
Space
- Stored state: O(S + E) (dominant)
- Peak temp: O(max out(v))
So:
- O(S + E) space overall, with extra O(max out(v)) transient.
// NOTE - records are immutibable (so reference here is immutable but references a mutable set)
// find because we're not hashing or anything, would use class otherwise
public static record EntityData(String name, Set<String> sentTo, Set<String> receivedFrom) {
public int countDistinctUnrepliedRecipients() {
int count = 0;
for (String r : sentTo) {
if (!receivedFrom.contains(r)) count++;
}
return count;
}
}
/**
* TODO: Implement me.
*
* Return all senders A such that countDistinctUnrepliedRecipients(A) >= T,
* where recipient B is counted as "unreplied" if there is NO event (B -> A) in the batch.
*/
public static Set<String> findSpammersUnreplied(List<Event> events, int T) {
Set<String> spammers = new HashSet<String>();
if (events == null || events.isEmpty()) return spammers;
// if T < 0, set T = 1;
int threshold = Math.max(T, 1);
// build map of senders -> {set of unique sentTo, set of unique receivedFrom}
Map<String, EntityData> senderDataMap = new HashMap<>();
for (Event event : events) {
if (event == null) continue; // TODO metrics?
String sender = event.sender;
String recipient = event.recipient;
if (sender == null || sender.isEmpty()
|| recipient == null || recipient.isEmpty()
|| sender.equals(recipient)) continue; // TODO metrics?
// update sender
EntityData senderData = senderDataMap.computeIfAbsent(sender, k ->
new EntityData(sender, new HashSet<>(), new HashSet<>()));
senderData.sentTo().add(recipient);
// update receiver
EntityData recipientData = senderDataMap.computeIfAbsent(recipient, k ->
new EntityData(recipient, new HashSet<>(), new HashSet<>()));
recipientData.receivedFrom().add(sender);
}
// iterate map, identify unreciprocated messages >= T
for (Map.Entry<String, EntityData> entry : senderDataMap.entrySet()) {
if (entry.getValue().countDistinctUnrepliedRecipients() >= threshold) {
spammers.add(entry.getKey());
}
}
// sorting?
return spammers;
}
Streamed Spammer
public static class SpammerDetector {
private final int spammerThreshold;
// Map entity to other unique entities they have contacted
private final Map<String, Set<String>> entityContacts;
private Set<String> identifiedSpammers;
public SpammerDetector(int T) {
this.spammerThreshold = Math.max(T, 1);
entityContacts = new HashMap<>();
identifiedSpammers = new HashSet<>();
}
public void onEvent(String sender, String recipient) {
if (sender == null || sender.isEmpty()
|| recipient == null || recipient.isEmpty()
|| sender.equals(recipient)
|| identifiedSpammers.contains(sender)) {
return;
}
Set<String> contacts = entityContacts.computeIfAbsent(sender, k -> new HashSet<>());
contacts.add(recipient);
if (contacts.size() >= spammerThreshold) {
identifiedSpammers.add(sender);
entityContacts.remove(sender);
}
}
public boolean isSpammer(String sender) {
if (sender == null || sender.isEmpty()) return false;
return identifiedSpammers.contains(sender);
}
/**
* Optional but recommended (tests will use it).
* If you don’t want to implement it, you can return Collections.emptySet()
* and comment out tests that reference it.
*/
public Set<String> currentSpammers() {
// defensive return, don't allow mutation
return new HashSet<>(identifiedSpammers);
}
}
Windowed Stream Spammer
Let m be number of events for a particular sender.
onEvent: O(1) average + expiry. Each event is removed once, so total expiry work over m events is O(m). → amortized O(1) per event.isSpammer: also amortized O(1) if called with non-decreasingnowMillis(or at least not rewinding time), because expirations happen once.
Space per sender:
- deque holds events still in window: up to number of events in last W
- freq map holds distinct recipients in window.
public static class WindowedUniqueRecipientDetector {
private static final record MessageEvent(String sender, String recipient, long timestampMs) {}
private static final class EntityCommData {
private final Deque<MessageEvent> messageQueue;
private final Map<String, Integer> receiverCounts;
private int uniqueReceivers;
public EntityCommData() {
messageQueue = new ArrayDeque<>();
receiverCounts = new HashMap<>();
uniqueReceivers = 0;
}
public void onMessageEvent(MessageEvent messageEvent) {
int currentCountForReceiver = receiverCounts.getOrDefault(messageEvent.recipient, 0);
// adding first count, new receiver
if (currentCountForReceiver == 0) uniqueReceivers++;
currentCountForReceiver++;
messageQueue.addFirst(messageEvent);
receiverCounts.put(messageEvent.recipient, currentCountForReceiver);
}
public void removeOlderThan(long timestampMs) {
while(messageQueue.size() > 0 && messageQueue.peekLast().timestampMs <= timestampMs) {
MessageEvent event = messageQueue.removeLast();
int currentCountForReceiver = receiverCounts.get(event.recipient);
if (currentCountForReceiver == 1) {
receiverCounts.remove(event.recipient);
uniqueReceivers--;
} else {
receiverCounts.put(event.recipient, currentCountForReceiver - 1);
}
}
}
int getUniqueReceivers() { return uniqueReceivers; }
}
private final long windowMs;
private final int spammerThreshold;
private Map<String, EntityCommData> entityCommDataMap;
public WindowedUniqueRecipientDetector(int T, long windowMillis) {
this.windowMs = windowMillis;
this.spammerThreshold = Math.max(T, 1);
entityCommDataMap = new HashMap<>();
}
public void onEvent(String sender, String recipient, long timestampMillis) {
if (sender == null || sender.isEmpty()
|| recipient == null || recipient.isEmpty()
|| recipient.equals(sender)
|| timestampMillis < 0)
return;
EntityCommData senderCommData = entityCommDataMap.computeIfAbsent(sender, k -> new EntityCommData());
MessageEvent messageEvent = new MessageEvent(sender, recipient, timestampMillis);
senderCommData.onMessageEvent(messageEvent);
// clean up window as we progress
long oldestTimestampInWindowMs = timestampMillis - windowMs;
senderCommData.removeOlderThan(oldestTimestampInWindowMs);
// remove entity tracking from map if sender hasn't communicated in window
if (senderCommData.getUniqueReceivers() == 0) entityCommDataMap.remove(sender);
}
public boolean isSpammer(String sender, long nowMillis) {
if (sender == null || sender.isEmpty()
|| nowMillis < 0
) return false;
EntityCommData senderCommData = entityCommDataMap.get(sender);
if (senderCommData == null) return false;
long oldestTimestampInWindowMs = nowMillis - windowMs;
senderCommData.removeOlderThan(oldestTimestampInWindowMs);
int currentUniqueReceivers = senderCommData.getUniqueReceivers();
// clean up map as we progress
if (currentUniqueReceivers == 0) {
entityCommDataMap.remove(sender);
return false;
}
return currentUniqueReceivers >= spammerThreshold;
}
}
public record MessageCounts(Set<Integer> out, Set<Integer> in) {}
public static int findSpammer(int N, int[][] messages) {
if (N <= 0) return -1;
if (N == 1) return 1;
if (messages == null) return -1;
Map<Integer, MessageCounts> map = new HashMap<>();
for (int[] m : messages) {
if (m == null || m.length < 2) continue;
int from = m[0], to = m[1];
if (from < 1 || from > N || to < 1 || to > N || from == to) continue;
map.computeIfAbsent(from, k -> new MessageCounts(new HashSet<>(), new HashSet<>()))
.out().add(to);
map.computeIfAbsent(to, k -> new MessageCounts(new HashSet<>(), new HashSet<>()))
.in().add(from);
}
for (int i = 1; i <= N; i++) {
MessageCounts c = map.get(i);
int outD = (c == null) ? 0 : c.out().size();
int inD = (c == null) ? 0 : c.in().size();
if (outD == N - 1 && inD == 0) return i;
}
return -1;
}
More Targeted Hubspot
notes:
- always check for validity (from == 2, invalid from/to, invalid message length)
Complexity is optimal:
- Time: O(N + M)
- Space: O(N)
// Return list of users in ascending order who have in-degree == 0.
public static List<Integer> neverReceived(int N, int[][] messages) {
List<Integer> ans = new ArrayList<Integer>();
int[] receivedCount = new int[N+1];
for (int[] message : messages) {
if (message == null || message.length != 2) continue;
int from = message[0];
int to = message[1];
if (to < 1 || to > N
|| from < 1 || from > N
|| from == to
) continue;
receivedCount[to]++;
}
for (int i = 1; i < receivedCount.length; i++) {
if(receivedCount[i] == 0) ans.add(i);
}
return ans;
}
notes
- don’t forget to check for edge cases, i.e. if N == 1, it has techincally “sent” to every other use
Complexity
- Time: O(M + E + Q log Q) where: (only sorting filtered list)
E= distinct edges stored in setsQ= number of qualifying users (sorting result)- Typically just say: O(M) expected + output sort
- Space: O(E)
// TODO: implement
// Return users who have sent to every other user at least once (distinct recipients == N-1).
// Return ascending order.
public static List<Integer> sentToEveryone(int N, int[][] messages) {
List<Integer> ans = new ArrayList<>();
if (N == 1) {
ans.add(1);
return ans;
}
if (messages == null || messages.length == 0) return ans;
Map<Integer, Set<Integer>> sentToMap = new HashMap<>();
for (int[] message : messages) {
if (message == null || message.length != 2) continue;
int from = message[0];
int to = message[1];
if (from < 1 || from > N
|| to < 1 || to > N
|| from == to
) continue;
Set<Integer> sentMap = sentToMap.computeIfAbsent(from, k -> new HashSet<>());
sentMap.add(to);
}
for (Map.Entry<Integer, Set<Integer>> entry : sentToMap.entrySet()) {
if (entry.getValue().size() == N - 1) ans.add(entry.getKey());
}
ans.sort(null);
return ans;
}
Notes
// TODO: implement
// Return users who sent >= T total messages (duplicates count), ascending order.
public static List<Integer> sentAtLeastT(int N, int[][] messages, int T) {
List<Integer> ans = new ArrayList<>();
if (messages == null || messages.length == 0) return ans;
int threshold = Math.max(T, 1);
int[] sentCount = new int[N+1];
for (int[] message : messages) {
if (message == null || message.length != 2) continue;
int from = message[0];
int to = message[1];
if (from < 1 || from > N
|| to < 1 || to > N
|| to == from
) continue;
sentCount[from]++;
}
for (int i = 1; i < N+1; i++) {
if (sentCount[i] >= threshold) ans.add(i);
}
return ans;
}
Top K
note
- can use
heap.comparator.compare()to use heaps comparator later - make sure to consider tie breaker!
- can
list.sort((a,b) -> {})for inplace sort
public static List<Integer> topKSenders(int N, int[][] messages, int K) {
List<Integer> ans = new ArrayList<Integer>();
if (K <= 0 || messages == null) return ans;
Map<Integer, Integer> sentMap = new HashMap<>();
for (int[] message : messages) {
if (message == null || message.length != 2) continue;
int from = message[0];
int to = message[1];
if (from < 1 || from > N
|| to < 1 || to > N
|| to == from
) continue;
sentMap.merge(from, 1, Integer::sum);
}
// int[0] == sender, int[1] == sendCount
PriorityQueue<int[]> senders = new PriorityQueue<>(
(a,b) ->{
int cmp = Integer.compare(a[1], b[1]); // count asc
if (cmp != 0) return cmp;
return Integer.compare(b[0], a[0]); // id desc (larger id is worse)
}
);
for (Map.Entry<Integer, Integer> entry : sentMap.entrySet()) {
int from = entry.getKey();
int count = entry.getValue();
int[] senderEntry = new int[]{from, count};
if (senders.size() < K) {
senders.offer(senderEntry);
} else {
if (senders.comparator().compare(senderEntry, senders.peek()) > 0) {
senders.poll();
senders.offer(senderEntry);
}
}
}
List<int[]> topKSendersList = new ArrayList<>(senders);
topKSendersList.sort((a,b) -> {
int cmp = Integer.compare(b[1], a[1]); // count desc
if (cmp != 0) return cmp;
return Integer.compare(a[0], b[0]); // id asc
});
List<Integer> res = new ArrayList<>();
for (int[] x : topKSendersList) res.add(x[0]);
return res;
}
top k spammers, descending order (tie ascening id)
Complexity (what you’d say)
- Build sets: O(M) expected time, O(E) space where E is distinct (from,to).
- Heap pass: O(S log K) where S is number of senders in map.
- Final sort: O(K log K).
public static List<Integer> topKSpammers(int N, int[][] messages, int T, int K) {
List<Integer> ans = new ArrayList<>();
if (K <= 0 || messages == null || messages.length == 0) return ans;
Map<Integer, Set<Integer>> sentToMap = new HashMap<>();
int threshold = Math.max(T, 1);
for (int[] message : messages) {
if (message == null || message.length != 2) continue;
int from = message[0];
int to = message[1];
if (from < 1 || from > N
|| to < 1 || to > N
|| from == to
) continue;
Set<Integer> sentToSet = sentToMap.computeIfAbsent(from, k -> new HashSet<>());
sentToSet.add(to);
}
// int[0] == id, int[1] == count
PriorityQueue<int[]> heap = new PriorityQueue<>((a,b) -> {
int cmp = Integer.compare(a[1], b[1]);
if (cmp != 0) return cmp;
else return Integer.compare(b[0], a[0]);
});
for (Map.Entry<Integer, Set<Integer>> mapEntry : sentToMap.entrySet()) {
int from = mapEntry.getKey();
Set<Integer> sentToSet = mapEntry.getValue();
int[] entry = new int[]{from, sentToSet.size()};
// not a spammer
if (sentToSet.size() < threshold) continue;
// is spammer, track top K
if (heap.size() < K) {
heap.offer(entry);
} else {
if (heap.comparator().compare(entry, heap.peek()) > 0) {
heap.poll();
heap.offer(entry);
}
}
}
List<int[]> topKSpammers = new ArrayList<>(heap);
topKSpammers.sort((a,b) -> {
int cmp = Integer.compare(b[1], a[1]);
if (cmp != 0) return cmp;
else return Integer.compare(a[0], b[0]);
});
for(int[] spammer : topKSpammers) ans.add(spammer[0]);
return ans;
}
all celebts
private static final record CommData(Integer node, Set<Integer> out, Set<Integer> in){}
public static List<Integer> findAllCelebrities(int N, int[][] messages) {
List<Integer> ans = new ArrayList<>();
if (N==1) {
ans.add(1);
return ans;
}
if (messages == null || messages.length == 0) return ans;
Map<Integer, CommData> sentToMap = new HashMap<>();
for (int[] message : messages) {
if (message == null || message.length != 2) continue;
int from = message[0];
int to = message[1];
if (from < 1 || from > N
|| to < 1 || to > N
|| from == to
) continue;
CommData senderCommData = sentToMap.computeIfAbsent(from, k -> new CommData(k, new HashSet<>(), new HashSet<>()));
senderCommData.out().add(to);
CommData receiverCommData = sentToMap.computeIfAbsent(to, k -> new CommData(k, new HashSet<>(), new HashSet<>()));
receiverCommData.in().add(from);
}
for (Map.Entry<Integer, CommData> mapEntry : sentToMap.entrySet()) {
int from = mapEntry.getKey();
CommData commData = mapEntry.getValue();
// not a spammer
if (!(commData.in().size() == N-1 && commData.out().size() == 0)) continue;
ans.add(from);
}
ans.sort(null);
return ans;
}
MongoDB
Group strings by anagram
approach
- compute signature, map by signature
private static int computeStringSig(String str) {
int[] chars = new int[26];
for (char c : str.toCharArray()) {
chars[c - 'a']++;
}
return Arrays.hashCode(chars);
}
// =========================
// TODO: Implement this
// =========================
/**
* TODO
* - makeup of strings
* - lowercase chars a-z
*/
public static List<List<String>> groupAnagrams(String[] strs) {
List<List<String>> ans = new ArrayList<>();
// return empty
if (strs == null || strs.length == 0) return ans;
// maps signature -> list (where signature represents all chars in strings)
Map<Integer, List<String>> ansMap = new HashMap<>();
for (String str : strs) {
int signature = computeStringSig(str);
List<String> stringsForSig = ansMap.computeIfAbsent(signature, k -> new ArrayList<>());
stringsForSig.add(str);
}
for (Map.Entry<Integer, List<String>> entry : ansMap.entrySet()) {
ans.add(entry.getValue());
}
return ans;
}
Find Max Average in K sublist
public static double findMaxAverage(int[] nums, int k) {
if (nums == null || nums.length == 0) return 0.0;
if (k <= 0 || k > nums.length) throw new IllegalArgumentException("Invalid k");
long sum = 0;
for (int i = 0; i < k; i++) sum += nums[i];
long maxSum = sum;
for (int i = k; i < nums.length; i++) {
sum += nums[i];
sum -= nums[i - k];
if (sum > maxSum) maxSum = sum;
}
return (double) maxSum / k;
}
KSum
- use recursion and 2 sum
- if greater than 2 sum, iterate and recurse
public static List<List<Integer>> kSum(int[] nums, int k, int target) {
if (nums == null) return List.of();
if (k <= 0 || k > nums.length) throw new IllegalArgumentException("Invalid k");
Arrays.sort(nums);
return kSumFrom(nums, 0, k, (long) target);
}
private static List<List<Integer>> kSumFrom(int[] nums, int start, int k, long target) {
int n = nums.length;
List<List<Integer>> res = new ArrayList<>();
if (k == 0) return res;
if (start >= n) return res;
// Base case: 1-sum (unique values only)
if (k == 1) {
for (int i = start; i < n; i++) {
if (i > start && nums[i] == nums[i - 1]) continue;
if ((long) nums[i] == target) res.add(List.of(nums[i]));
}
return res;
}
// Base case: 2-sum via two pointers (unique pairs)
if (k == 2) {
int l = start, r = n - 1;
while (l < r) {
if (l > start && nums[l] == nums[l - 1]) { l++; continue; }
if (r < n - 1 && nums[r] == nums[r + 1]) { r--; continue; }
long sum = (long) nums[l] + nums[r];
if (sum == target) {
res.add(Arrays.asList(nums[l], nums[r]));
l++;
r--;
} else if (sum < target) {
l++;
} else {
r--;
}
}
return res;
}
// Optional pruning (helps a lot on big inputs)
// Compute min possible sum with k numbers from start: nums[start] * k (lower bound)
// Compute max possible sum with k numbers from end: nums[n-1] * k (upper bound)
long minPossible = (long) nums[start] * k;
long maxPossible = (long) nums[n - 1] * k;
if (target < minPossible || target > maxPossible) return res;
// Recursive case: fix one number, solve (k-1)-sum for remainder
for (int i = start; i <= n - k; i++) {
if (i > start && nums[i] == nums[i - 1]) continue;
long newTarget = target - nums[i];
// Additional pruning per choice (optional)
long minWithI = (long) nums[i] + (long) nums[i + 1] * (k - 1);
long maxWithI = (long) nums[i] + (long) nums[n - 1] * (k - 1);
if (newTarget < (long) nums[i + 1] * (k - 1) && minWithI > target) break; // too big, and will only grow
if (maxWithI < target) continue; // too small, try larger i
List<List<Integer>> tails = kSumFrom(nums, i + 1, k - 1, newTarget);
for (List<Integer> tail : tails) {
ArrayList<Integer> combo = new ArrayList<>(k);
combo.add(nums[i]);
combo.addAll(tail);
res.add(combo);
}
}
return res;
}
alternative
The worst-case time complexity is O(n^(k−1)) since we recurse k−2 levels and finish with a linear two-sum. Space complexity is O(k) for recursion, plus the space needed to store the results
public static List<List<Integer>> kSum(int[] nums, int k, int target) {
if (nums == null) return List.of();
if (k <= 0 || k > nums.length) throw new IllegalArgumentException("Invalid k");
Arrays.sort(nums);
return helper(nums, 0, k, (long) target);
}
private static List<List<Integer>> helper(int[] nums, int start, int k, long target) {
List<List<Integer>> res = new ArrayList<>();
int n = nums.length;
if (k == 2) {
int l = start, r = n - 1;
while (l < r) {
if (l > start && nums[l] == nums[l - 1]) { l++; continue; }
if (r < n - 1 && nums[r] == nums[r + 1]) { r--; continue; }
long sum = (long) nums[l] + nums[r];
if (sum == target) {
res.add(Arrays.asList(nums[l], nums[r]));
l++;
r--;
} else if (sum < target) {
l++;
} else {
r--;
}
}
return res;
}
for (int i = start; i <= n - k; i++) {
if (i > start && nums[i] == nums[i - 1]) continue;
for (List<Integer> tail : helper(nums, i + 1, k - 1, target - nums[i])) {
ArrayList<Integer> combo = new ArrayList<>(k);
combo.add(nums[i]);
combo.addAll(tail);
res.add(combo);
}
}
return res;
}
Can Finish Course
- use a state array 0 = not visited, 1 = visiting, 2 = done (safe)
- look at
hasCycle()!
public static boolean canFinish(int n, int[][] prerequisites) {
Map<Integer, List<Integer>> adjMap = new HashMap<>();
for (int[] prereq : prerequisites) {
if (prereq == null || prereq.length!= 2) continue;
int course = prereq[0];
int dep = prereq[1];
if (course < 0 || course >= n
|| dep < 0 || dep >= n
) continue; // or throw
if (course == dep) return false;
List<Integer> adj = adjMap.computeIfAbsent(dep, k -> new ArrayList<>());
adj.add(course);
}
// state 0 = unvisited, 1 = visiting, 2 = done (safe)
int[] state = new int[n];
for (int i = 0; i < n; i++) {
if (state[i] == 0 && hasCycle(i, state, adjMap)) return false;
}
return true;
}
private static boolean hasCycle(int course, int[] state, Map<Integer, List<Integer>> adjMap) {
state[course] = 1;
if (adjMap.containsKey(course)) {
for (int neighbor : adjMap.get(course)) {
if (state[neighbor] == 1) return true;
if (state[neighbor] == 0 && hasCycle(neighbor, state, adjMap)) return true;
}
}
state[course] = 2;
return false;
}